LXF77:MetaPost
|
|
|
- Метамодернизм в позднем творчестве В.Г. Сорокина
- ЛитРПГ - последняя отрыжка постмодерна
- "Ричард III и семиотика"
- 3D-визуализация обложки Ridero создаем обложку книги при работе над самиздатом.
- Архитектура метамодерна - говоря о современном искусстве, невозможно не поговорить об архитектуре. В данной статье будет отмечено несколько интересных принципов, характерных для построек "новой волны", столь притягательных и скандальных.
- Литература
- Метамодерн
- Рокер-Прометей против изначального зла в «Песне про советскую милицию» Вени Дркина, Автор: Нина Ищенко, к.ф.н, член Союза Писателей ЛНР - перепубликация из журнала "Топос".
- Как избавиться от комаров? Лучшие типы ловушек.
- Что делать если роблокс вылетает на windows
- Что делать, если ребенок смотрит порно?
- Почему собака прыгает на людей при встрече?
- Какое масло лить в Задний дифференциал (мост) Visco diff 38434AA050
- О чем может рассказать хвост вашей кошки?
- Верветки
- Отчетность бюджетных учреждений при закупках по Закону № 223-ФЗ
- Срок исковой давности как правильно рассчитать
- Дмитрий Патрушев минсельхоз будет ли преемником Путина
- Кто такой Владислав Поздняков? Что такое "Мужское Государство" и почему его признали экстремистским в России?
- Как правильно выбрать машинное масло в Димитровграде?
- Как стать богатым и знаменитым в России?
- Почему фильм "Пипец" (Kick-Ass) стал популярен по всему миру?
- Как стать мудрецом?
- Как правильно установить FreeBSD
- Как стать таким как Путин?
- Где лучше жить - в Димитровграде или в Ульяновске?
- Почему город Димитровград так называется?
- Что такое метамодерн?
- ВАЖНО! Временное ограничение движения автотранспортных средств в Димитровграде
- Тарифы на электроэнергию для майнеров предложено повысить
Содержание[убрать] |
MetaPost Базовые элементы
Определённо всё из чего-то состоит. Элементарные кирпичики – вот что интересно. Евгений Балдин продолжает уроки рисования.
Объяснять компьютеру что Вы хотите сделать гораздо сложнее, чем нарисовать самому. Компьютеру надо объяснять абсолютно всё – телепатические способности у машин на текущий момент отсутствуют. Но, объяснив один раз, все похожие действия выполняются путём небольшой модификации уже готовых инструкций. В результате, потраченное на объяснение время себя полностью оправдывает, правда, при этом требуются дополнительные «мозговые усилия».
Рисуем по точкам
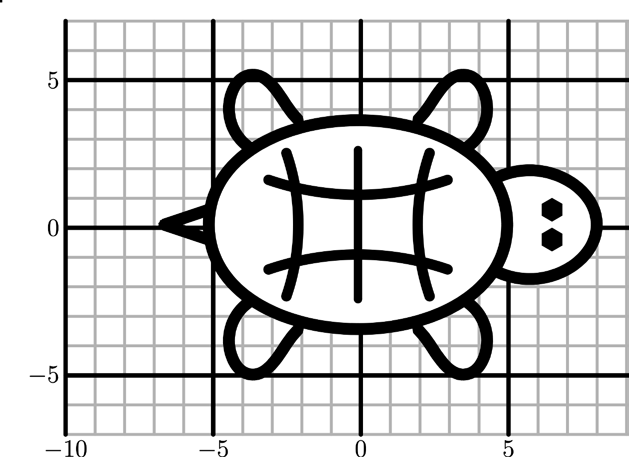
Первое, что надо сделать перед созданием нового рисунка, это сделать его набросок на миллиметровке. Допустим, необходимо нарисовать черепашку:
Делаем это, как можем, а затем очень подробно объясняем компьютеру, что мы хотим от него. Инструкции очень простые:
%Файл coord.mp %Черепашка beginfig(1) ; numeric u;u:=5mm; draw (-5u,0u){dir 90}..{dir 0}(0,3.5u){dir0}.. {dir -90}(5u,0){dir -90}..{dir 180}(0u,-3.5u){dir 180}.. {dir 90}cycle withpen pencircle scaled 0.4u; draw (4.5u,1.5u)..(7u,1.5u)..(8u,0u)..(7u,-1.5u).. (4.5u,-1.5u) withpen pencircle scaled 0.4u; draw (6.5u,.5u) withpen pencircle scaled 0.8u; draw (6.5u,-.5u) withpen pencircle scaled 0.8u; draw (-3.5u,-2.5u)..(-4.2u,-4.5u)..(-3.7u,-5u).. (-2.4u,-4u)..(-2u,-3.5u) withpen pencircle scaled 0.4u; draw (-3.5u,2.5u)..(-4.2u,4.5u)..(-3.7u,5u)..(-2.4u,4u).. (-2u,3.5u) withpen pencircle scaled 0.4u; draw (3.5u,-2.5u)..(4.2u,-4.5u)..(3.7u,-5u)..(2.4u,-4u).. (2u,-3.5u) withpen pencircle scaled 0.4u; draw (3.5u,2.5u)..(4.2u,4.5u)..(3.7u,5u)..(2.4u,4u).. (2u,3.5u) withpen pencircle scaled 0.4u; draw (-5u,0.5u)--(-6.5u,0)--(-5u,-0.5u) withpen pencircle scaled 0.4u; draw (0u,2.5u)..(0,0u)..(0u,-2.5u) withpen pencircle scaled 0.3u; draw (-2.4u,2.4u)..(-2u,0u)..(-2.4u,-2.4u) withpen pencircle scaled 0.3u; draw (2.4u,2.4u)..(2u,0u)..(2.4u,-2.4u) withpen pencircle scaled 0.3u; draw (-3u,1.5u)..(0,1u)..(3u,1.5u) withpen pencircle scaled 0.3u; draw (-3u,-1.5u)..(0,-1u)..(3u,-1.5u) withpen pencircle scaled 0.3u; endfig ;
Рисуем по точкам, используя команду draw. Каждая точка задаётся парой чисел «(x,y)» – x и y координаты соответственно. Точки соединяются либо прямыми линиями «--», либо кривыми «..». Кривые, соединяющие точки описываются полиномом Бернштейна третьей степени (Сергей Николаевич Бернштейн 1912). Часто их называют кубическими кривыми Безье (Piere Bezier 1960).
Компьютер обязательно должен знать каким пером (withpen pencircle) и какой толщины (scaled 0.3u) рисуется текущая линия. Такие объяснения могут показаться избыточными, но всегда можно скопировать предыдущую инструкцию и поправить её под свои нужды, а многословность облегчает чтение кода.
Далее этот рисунок можно использовать многократно, например, для составления какого-либо узора:
Обратите внимание, что почти все числовые значения представляют из себя коэффициент умноженный на параметр, например, «2.4u». Параметру «u» можно присвоить числовое значение в миллиметрах (параметр «mm»). Есть несколько определённых по умолчанию значений длины, например, «cm» соответствует сантиметру.
При программировании на Meta по мере возможности используйте параметрические зависимости. Нет необходимости «прибивать что-то гвоздями». В данном случае наличие параметра позволяет легко изменить масштаб рисунка:
Очевидно, что в предложенном решении одного параметра мало, так как «u» контролирует не только геометрические размеры, но и размеры пера. Точки, также можно представить как переменные, имеющие тип pair:
numeric u; u:=0.5mm; pair A,B; A:=(1u,2u);B=(5u,10u); draw A--B withpen pencircle scaled 0.3u;
Следует обратить внимание, что знак присвоения «:=» в случае переменной A и знак равенства в случае переменной B здесь действует одинаково. Отличия возникают, когда используется уникальная способность Meta воспринимать и решать систему линейных уравнений. В дальнейшем в объяснениях буквы A и B будут использоваться как переменные типа точка.
Meta позволяет создавать свои типы перьев, но для рисования простых рисунков использовать что-то отличное от круглого пера (pencircle) нет особой необходимости. Если вам хочется расширить ваши познания в этой области, то обратитесь к любому руководству по MetaFont или MetaPost. Нет необходимости каждый раз указывать каким пером следует рисовать. Достаточно выбрать какое-либо перо по умолчанию с помощью команды pickup, например, так:
pickup pencircle scaled 0.2u;
Пути
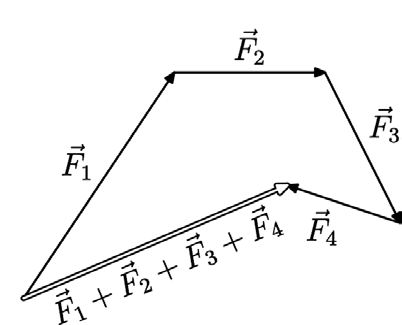
Инструкции draw позволяет рисовать сплошную линию. На её основе в MetaPost создана команда для рисования стрелки drawarrow. Воспользуемся ей для изображения суммы векторов (рис. справа)
Кроме непосредственно команды draw, в этом рисунке необходимо использовать команду для вставки текстовых меток label, которая будет подробно разобрана позже:
%Файл path.mp %Закон Ньютона - векторная сумма сил beginfig(1); numeric u; u := 1mm; drawarrow (0,0)--(20u,30u) withpen pencircle scaled 0.3u; label.ulft(btex \(\vec{F}_1\) etex,1/2[(0,0),(20u,30u)]); drawarrow (20u,30u)--(40u,30u) withpen pencircle scaled 0.3u; label.top(btex \(\vec{F}_2\) etex,1/2[(20u,30u),(40u,30u)]); drawarrow (40u,30u)--(50u,10u) withpen pencircle scaled 0.3u; label.urt(btex \(\vec{F}_3\) etex,1/2[(40u,30u),(50u,10u)]); drawarrow (50u,10u)--(35u,15u) withpen pencircle scaled 0.3u; label.llft(btex \(\vec{F}_4\) etex,1/2[(50u,10u),(35u,15u)]); drawarrow (0u,0u)--(35u,15u) withpen pencircle scaled 0.8u; drawarrow (0u,0u)--(35u,15u) withpen pencircle scaled 0.3u withcolor white; draw (0u,0u) withpen pencircle scaled 2u ; label.bot(btex \(\vec{F}_1+\vec{F}_2+\vec{F}_3+\vec{F}_4\) etex, 1/2[(35u,15u),(0u,0u)]) rotatedaround (1/2[(35u,15u),(0u,0u)],angle(35,15)); endfig;
Конструкция вида «1/2[A,B]» имеет тип pair и равна точке, расположенной ровно по середине между точками A и B. Точно так же можно выбрать точку на линии AB, но делящую эту линию в отношении 1 к 2: «1/3[A,B]», или 1 к 4: «0.2[A,B]»
Кроме drawarrow в MetaPost определена команда drawdblarrow, которая рисует кончик стрелки на обоих концах пути.
Команды, типа draw, работают с объектами path (путь). Путь – это набор из точек (тип pair) с описанием того, как эти точки соединяются друг с другом. Минимальный путь – это одна точка. При рисовании такого пути на рисунке остаётся отпечаток в форме пера. Во всех приведённых здесь примерах перо имеет круглую форму pencircle, поэтому в этом случае возникает просто точка. Часто бывает удобно создать переменную типа path:
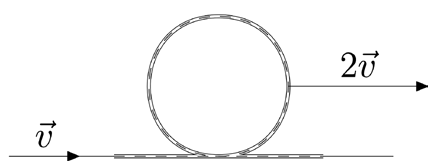
%Файл path.mp %Рис к 1.6.8 б) нить пропущенная через изогнутую трубу beginfig(2) ; numeric u; u = 0.8mm; path p; p:=(5u,0u)--(20u,0u){dir 0}..(20u,20u).. {dir 0}(20u,0u)--(35u,0u); cutdraw p withpen pencircle scaled 1.5u; draw p withpen pencircle scaled 1u withcolor white; draw p withpen pencircle scaled 0.3u dashed evenly scaled 1/2u; drawarrow (-10u,0u)--(0u,0u) withpen pencircle scaled 0.3u; draw (-10u,0u) withpen pencircle scaled 1u; draw (-10u,0u)--(5u,0u) withpen pencircle scaled 0.3u; drawarrow (30u,10u)--(50u,10u) withpen pencircle scaled 0.3u; draw (30u,10u) withpen pencircle scaled 1u; draw (35u,0u)--(45u,0u) withpen pencircle scaled 0.3u; label.top(btex \(\vec{v}\) etex,(-5u,0u)); label.top(btex \(2\vec{v}\) etex,(40u,10u)); endfig;
В данном примере требовалось изобразить трубу изогнутую буквой «О», сквозь которую продета нить. Для этого определяем путь «p». Затем этот путь используется в трёх командах как переменная: рисуется толстая чёрная труба шириной «1.5u», внутри неё рисуется более тонкая шириной «1u» белого цвета (withcolor white) – получается полая труба, а затем внутри трубы отрисовывается нить, причём нить рисуется пунктиром (dashed evenly).
Первый и последний участок изогнутой трубы прямые линии, поэтому соединение с первой и последней точкой описывается как «--». Чтобы нарисовать кривую, похожую на круг, достаточно двух точек:
numeric u,R; u=1mm;R=10u; pair A,B; A:=(-R,0);B:=(0,R); path P; P:=A..B..cycle; draw P withpen pencircle 1u;
В этом примере определяются две точки A и B. Путь P строится по этим точкам, при этом выходя из точки A, мы попадаем в точку B, а затем снова в точку A: команда cycle позволяет создавать замкнутую кривую. Настройки Meta по умолчанию таковы, что получившаяся кривая достаточно хорошо совпадает с точной окружностью. Чтобы лучше совпадать с окружностью нужно больше «опорных» точек. Для обычных рисунков хватает точности построения по двум точкам, но всё-таки надо осознавать, что отличие есть.
Для уточнения пути в некоторых точках можно указать под каким углом должна подходить кривая к этой точке. Инструкция вида «dir » если она находится перед точкой, указывает под каким углом кривая должна подходить, а после точки – под каким углом кривая должна уходить. – угол в градусах от оси абсцисс.
Для указания направления можно так же воспользоваться сокращениями left, right, up и down, которые означают, соответственно, влево, вправо, вверх и вниз.
Существует несколько типов соединений между точками. Два из них «..» и «--» мы уже изучили. Из других типов полезен тип «&» – «сращивание» (объединение двух путей без влияния друг на друга) и «---» – «натянутая» линия (то же, что и «--», но влияет на соседние соединительные участки).
Обратите внимания на команду cutdraw. Так как MetaPost рисует с помощью перьев, то в случае круглого пера (pencircle), концы линий также округлые. В случае, когда необходимо «обрубить» концы, избавиться от округлостей на концах линий, и используется эта инструкция. Следует отметить, что эта команда «подчистки» концов использует другую более общую команду
cutoff(«точка»,«угол»);
Вставка текста
MetaFont был создан как специализированный инструмент для создания шрифтов. MetaPost создавался как инструмент для рисования любых изображений, поэтому в него был встроен довольно мощный механизм вставки текста. Работая совместно с LaTeX, MetaPost позволяет использовать всю мощь текстового процессора для создания надписей. Кроме всего прочего, иметь в рисунках те же шрифты, что и в тексте просто красиво.
Разберём это на примере треугольник Паскаля – треугольной числовой таблицы для составления биномиальных коэффициентов. По боковым сторонам треугольника стоят единицы, внутри треугольника числа образуются сложением двух чисел, стоящих над данным:
Так как нижние строки из-за увеличения разрядности чисел расползались, то для представления появилась необходимость уменьшить их геометрические размеры. В коде так же использовались циклы, которые будут разобраны позже. Команда show позволяет отлаживать код, выдавая значения переменных на экран во время компиляции рисунка с помощью mpost.
%Файл pic.mp %Треугольник Паскаля beginfig(5) ; numeric u; u = 1.mm; numeric dy,dx,x,y,n[ ][ ],i,j,sy,ds,nlast; dy:=5u;dx:=5u;x=0;y=0; ds=0.04;sy=0.032;nlast=14; picture z; for i:=0 upto nlast: dy:=dy*(1-sy); y:=y-dy; for j:=0 upto i: if (j=0) or (j=i): n[i][j]:=1; else: n[i][j]:=n[i-1][j-1]+n[i-1][j]; fi % show i,j,n[i][j]; z:=thelabel(decimal(n[i][j]),(0,0)); x:=dx*(j-i/2); label(z scaled (1-ds*i),(x,y)); endfor z:=thelabel.lft(decimal(i)&”:”,(0,0)); label(z scaled (1-ds*i),(dx*(-nlast/2-1),y)); endfor label.rt(btex \((a+b)^n=\) etex,(5u,-5u)); label.rt(btex \(=\sum C^k_na^kb^{n-k}\) etex, (10u,-10u)); label.lft(btex Треугольник Паскаля etex rotated 56,(-5u,-20u)); endfig ;
Команда decimal делает из переменной типа numeric строку. Две строки можно слить с помощью операнда «&».
Для того чтобы вставить текстовую метку в рисунок, необходимо получить на входе текстовую строку, которую, возможно, надо будет преобразовать с помощью LaTeX, и точку где эту строку следует расположить:
label(“text string”,A);
Полезно ещё уточнить с какой стороны от указанной точки расположить текстовую метку. Уточнение производится с помощью суффикса, который добавляется макросу label через точку. Всего существует восемь стандартных суффиксов: «.rt» – расположить справа, «.lft» – слева, «.top» – сверху, «.bot» – снизу, «.llft» – расположить снизу и слева по диагонали, «.lrt» – снизу и справа, «.ulft» – сверху и слева, «.urt» – сверху и справа.
Если label передаётся просто строка (тип string), то текст обрабатывается силами MetaPost и всё, что выходит за пределы ASCII-таблицы с большой вероятностью не отобразится. Для того чтобы строка была обработана LaTeX, необходимо указать это с помощью разделителей btex и etex. Строка между этими разделителями обрабатывается LaTeX, при этом в качестве заголовка используются инструкции перечисленные в начале mp-файла между verbatimtex и etex. Таким образом можно использовать кириллицу и любую конструкцию, которую понимает LaTeX.
В некоторых случаях команде label удобно передавать не строку, а картинку picture. В нашем случае это было необходимо, так как надпись надо было масштабировать. Объект picture представляет из себя совокупность примитивов типа путей и точек, поэтому его можно трансформировать. Команда thelabel создаёт такую картинку. Объект, заключённый между btex и etex так же является картинкой.
Заливка
Кроме рисования кривых часто бывает необходимо закрасить какую-либо замкнутую область. Для этого сущест- вует команда fill. На вход команды fill подаётся объект типа path, при этом путь должен быть замкну- тым, то есть оканчи- ваться командой cycle. Команда cycle автоматически замыкает кривую.
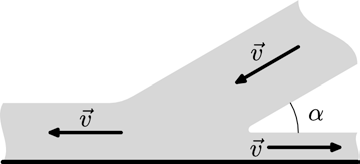
%Файл pic.mp %Рис к 1.6.20 а) струя под углом, разбивающаяся о пол beginfig(10) ; numeric u; u = 1mm; numeric st;st:=u/(sqrt 3); path p; p:=(0,10u)--(18u,10u){dir 0}..{dir 30}(22u,10u+2st)-- (50u,10u+30st){dir -90}..{dir -90}(60u,5u+20st)-- (42u,5u+2st){dir -150}..{dir 0}(42u,5u)-- (60u,5u){dir -120}..{dir -120}(60u,0u)-- (0u,0u){dir 60}..{dir 60}cycle; fill p withcolor 0.8 white; draw ((40u,5u)+10u*dir 30){dir -60}..{dir -90}(50u,5u); label(btex \(\alpha\) etex,(53u,8u)); draw (0u,0)--(60u,0u) withpen pencircle scaled 0.8u; numeric R,alpha;R:=12u;alpha=30; drawarrow (25u+25u,5u+25st)-- ((25u+25u,5u+25st)-R*dir alpha) withpen pencircle scaled 0.6u; label.ulft(btex \(\vec{v}\) etex,1/2[(25u+25u,5u+25st), ((25u+25u,5u+25st)-R*dir alpha)]); drawarrow (20u,5u)--(20u-R,5u) withpen pencircle scaled 0.6u; label.top(btex \(\vec{v}\) etex,(20u-R/2,5u)); drawarrow (45u,2.5u)--(45u+R,2.5u) withpen pencircle scaled 0.6u; label.lft(btex \(\vec{v}\) etex,(45u,2.5u)); endfig ;
Для fill существует противоположная по смыслу команда unfill, которая, соответственно, убирает заливку в выбранной окрестности. Если вы планируете использовать эти команды, то изучите соответствующий раздел «Всё про METAFONT» Кнута, так как влияние этих команд друг на друга не совсем тривиально. Дело в том, что при наложении друг на друга двух заливок в месте пересечения образуется «двойной слой краски» и для того чтобы убрать его необходимо дважды вызывать команду unfill. Команда unfill действует схоже, только число «слоёв краски» становится отрицательным. Для сведения всё к ситуации когда краска либо есть (один слой), либо её нет используется команда «выравнивания» cullit.
Обратите внимание, что точку можно задать не только парой чисел: «(x,y)» – Декартова система координат, но и радиусом с направлением «R*dir » – полярные координаты.
Цвета
Ещё одно важное отличие MetaPost от MetaFont – это наличие цвета. Работа с цветом обычно сложнее, чем работа с чёрно-белым рисунком. До сих пор процедура переноса электронного цветного рисунка на бумагу не является тривиальной. Но время идёт, и цветные принтеры становятся всё доступней. Кроме того, хорошие чисто электронные тексты, не привязанные к твёрдой копии, так же становятся весьма распространёнными. Поэтому если необходимо, то следует пользоваться цветом, естественно, если вы знаете что делать. В случае простого рисунка цвет, как правило, только отвлекает.
В MetaPost управление цветом реализовано на довольно низком уровне. Цвет определяется объектом типа color и представляет из себя тройку чисел принимающих значение от 0 до 1: «(r,g,b)», где r соответствует красной, g – зелёной, а b – голубой компоненте. Существует пять предопределённых цветовых констант: red (1,0,0), green (0,1,0), blue (0,0,1), а так же black (1,1,1) и white (0,0,0).
Нарисовать объект, выбранным цветом, можно с помощью инструкции withcolor за которой следует сам цвет. Цвета можно складывать, вычитать, умножать на число. Пользуясь базовыми определениями можно создать более сложные объекта. Например как этот спектр:
Код, создающий эту картинку, далёк от совершенства, но он прост, и его можно улучшать в случае необходимости.
%Файл colors.mp def spectrline(expr ic,c,l,w,dw) = begingroup save i,ifirst,ilast,istep,icc; color icc; if (ic>0):istep:=1;ifirst:=0;ilast=255; else:istep:=-1;ifirst=0;ilast:=-255; fi; if (abs(ic)=1):icc:=red;fi; if (abs(ic)=2):icc:=green;fi; if (abs(ic)=3):icc:=blue;fi; for i:=ifirst step istep until ilast: draw ((0u,0u)--(0u,l)) shifted (w+(dw/2*abs(i),0)) withpen pencircle scaled dw withcolor (c+i/255*icc); endfor; endgroup; enddef; %спектр beginfig(1) ; color current; u:=1mm;w:=200u;dw:=w/512;l:=5u; current:=(1,0,0); spectrline(2,current,l,(1/4w,0u),dw) current:=(1,1,0); spectrline(-1,current,l,(1/2w,0u),dw) current:=(0,1,0); spectrline(3,current,l,(3/4w,0u),dw) current:=(0,1,1); spectrline(-2,current,l,(w,0u),dw) endfig ;
В примере используется макрос spectrline для уменьшения размера кода.