LXF157:Шко­ла LXF

Подписка на печатную версию Весь 2015 год (12 номеров) Первое полугодие (6 номеров) Второе полугодие (6 номеров)

Подписка на электронную версию Весь 2015 год (12 номеров) Первое полугодие (6 номеров) Второе полугодие (6 номеров)

Подшивки старых номеров журнала (печатные версии) Весь 2014 год (12 номеров) Первое полугодие (6 номеров) Второе полугодие (6 номеров)

Шко­ла LXF

Обмен опытом и передовые идеи по использованию свободного ПО в образовании

Взаи­мо­дей­ст­ву­ем с ок­ру­же­ни­ем, или И ро­бо­ты чув­ст­во­вать уме­ют

Тать­я­на Ка­зан­це­ва про­дол­жа­ет рас­ска­зы­вать о ро­бото­тех­ни­ке, ко­то­рая об­хо­дит­ся без ре­аль­ных ро­бо­тов.

• Метамодернизм в позднем творчестве В.Г. Сорокина
• ЛитРПГ - последняя отрыжка постмодерна
• "Ричард III и семиотика"
• 3D-визуализация обложки Ridero создаем обложку книги при работе над самиздатом.
• Архитектура метамодерна - говоря о современном искусстве, невозможно не поговорить об архитектуре. В данной статье будет отмечено несколько интересных принципов, характерных для построек "новой волны", столь притягательных и скандальных.
• Литература
• Метамодерн
• Рокер-Прометей против изначального зла в «Песне про советскую милицию» Вени Дркина, Автор: Нина Ищенко, к.ф.н, член Союза Писателей ЛНР - перепубликация из журнала "Топос".
• Как избавиться от комаров? Лучшие типы ловушек.
• Что делать если роблокс вылетает на windows
• Что делать, если ребенок смотрит порно?
• Почему собака прыгает на людей при встрече?
• Какое масло лить в Задний дифференциал (мост) Visco diff 38434AA050
• О чем может рассказать хвост вашей кошки?
• Верветки
• Отчетность бюджетных учреждений при закупках по Закону № 223-ФЗ
• Срок исковой давности как правильно рассчитать
• Дмитрий Патрушев минсельхоз будет ли преемником Путина
• Кто такой Владислав Поздняков? Что такое "Мужское Государство" и почему его признали экстремистским в России?
• Как правильно выбрать машинное масло в Димитровграде?
• Как стать богатым и знаменитым в России?
• Почему фильм "Пипец" (Kick-Ass) стал популярен по всему миру?
• Как стать мудрецом?
• Как правильно установить FreeBSD
• Как стать таким как Путин?
• Где лучше жить - в Димитровграде или в Ульяновске?
• Почему город Димитровград так называется?
• Что такое метамодерн?
• ВАЖНО! Временное ограничение движения автотранспортных средств в Димитровграде
• Тарифы на электроэнергию для майнеров предложено повысить

Се­го­дня речь пой­дет о дат­чи­ках, ко­то­рые по­зво­лят на­ше­му ро­бо­ту ори­ен­ти­ро­вать­ся в про­стран­ст­ве. В про­шлом вы­пуске Шко­лы (LXF156) мы на­ча­ли раз­би­рать­ся, как мож­но изу­чить осно­вы ро­бо­то­техники в усло­ви­ях, когда ре­аль­ные ро­бо­ты недоступ­ны. Мы нау­чи­ли ро­бо­та дви­гать­ся, ра­зо­бра­лись, как им мож­но управ­лять, и да­же уч­ли воз­мож­но­сти внесения ис­ка­жений в пе­ре­да­вае­мые ко­ман­ды.

Итак, мы нау­чим вир­ту­аль­ного ро­бо­та взаи­мо­дей­ст­во­вать с ок­ру­жением, осна­стив его дат­чи­ка­ми (конеч­но, то­же вир­ту­аль­ными), ко­то­рые бу­дут от­ра­жать ре­аль­но су­ще­ст­вую­щие ком­понен­ты при по­строении ре­аль­ных ро­бо­тов.

Коснись ме­ня

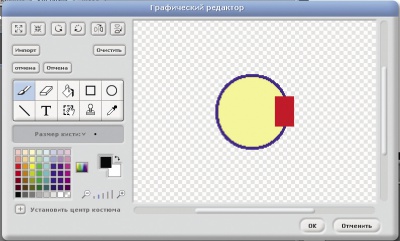
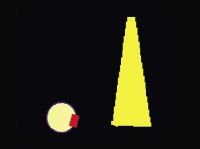
Са­мый про­стой дат­чик, ко­то­рым осна­ща­ют ро­бо­тов, это дат­чи­к ка­сания (или бам­пе­р). Такие датчики по­зво­ля­ют ро­бо­ту оп­ре­де­лять на­ли­чие пре­пят­ст­вий по хо­ду дви­жения, прико­снувшись к ним. Са­мый про­стой дат­чик – это дат­чик ка­сания, рас­по­ло­жен­ный по хо­ду дви­жения ро­бо­та.

Рис. 1. Вот так бу­дет вы­гля­деть наш ро­бот

Для де­мон­ст­ра­ции дви­жения нам по­на­до­бит­ся так­же вир­ту­аль­ный ла­би­ринт, по ко­то­ро­му наш ро­бот бу­дет разъезжать.

Ро­бот в на­шем слу­чае бу­дет пред­став­лять со­бой круг­лую плат­фор­му, спе­ре­ди ко­то­рой рас­по­лагается дат­чик ка­сания. Сра­зу сто­ит от­ме­тить, что ри­со­вать дат­чи­ки на­до на пра­вой сто­роне ро­бо­та, так как имен­но ту­да смот­рит на­прав­ление дви­жения 0.

Так­же нам по­на­до­бит­ся по­ле для его за­пуска, ко­то­рое в на­шем слу­чае бу­дет иметь вид про­стран­ст­ва, ок­ру­жен­но­го сплош­ным за­бо­ром.

Ал­го­ритм ро­бо­та бу­дет сле­дую­щим:

1 Ро­бот едет впе­ред, по­ка не коснет­ся за­бо­ра

2 Ес­ли сра­ба­ты­ва­ет дат­чик ка­сания, то ро­бот отъ­ез­жа­ет на­зад и по­во­ра­чи­ва­ет­ся на 90 гра­ду­сов по ча­со­вой стрел­ке.

3 Цикл по­вто­ря­ет­ся.

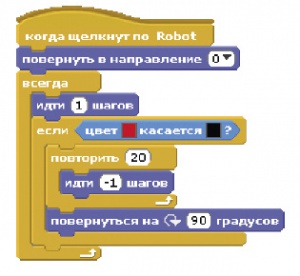
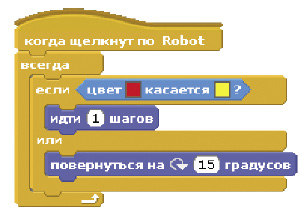
А про­грам­ма бу­дет та­кой:

За­пус­ка­ем мы ро­бо­та щелч­ком по нему (это по­зво­ля­ет нам по­ста­вить его в лю­бую точ­ку по­ля).

Как вид­но, мы ис­поль­зу­ем цвет дат­чи­ка (крас­ный) для оп­ре­де­ления со­при­косно­вения с цве­том сте­ны (синий). Это по­зво­лит нам в дальней­шем ис­поль­зо­вать несколь­ко дат­чи­ков.

Рис. 2. Заведем нашего ро­бота в лабиринт, и пусть он попробует добраться до упора.

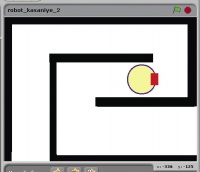
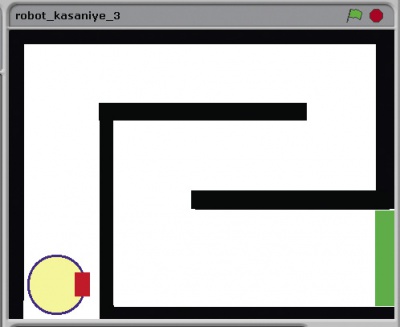
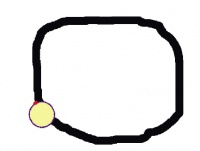
Ус­ложним за­да­чу. Ис­поль­зу­ем ла­би­ринт, показанный на рис. 2.

По­ста­вив ро­бо­та в его на­ча­ло и за­пустив, вы мо­же­те об­на­ру­жить, что он за­стрял в средней его час­ти и не мо­жет вы­брать­ся. Что же де­лать? По­про­бо­вать из­менить по­во­рот в на­прав­лении про­тив ча­со­вой стрел­ки? Тогда ро­бот бу­дет по­сто­ян­но воз­вра­щать­ся на­зад.

Мож­но сде­лать сле­дую­щее:

1 Столк­нув­шись со стен­кой, ро­бот по­во­ра­чи­ва­ет­ся впра­во и про­бу­ет по­ехать.

2 Ес­ли он сно­ва упи­ра­ет­ся в стен­ку за минималь­ное чис­ло дви­жения (к при­ме­ру, на ве­ли­чи­ну отъ­ез­да, ум­но­жен­ную на два), то он по­во­ра­чи­ва­ет­ся на 180 гра­ду­сов.

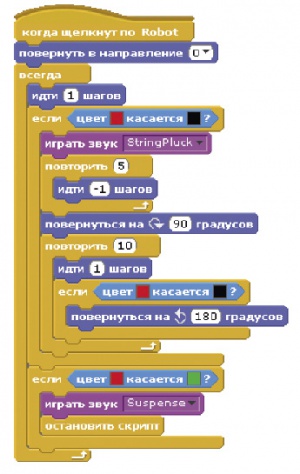
Ви­до­из­менен­ный код про­грам­мы бу­дет вы­гля­деть те­перь так.

Мы до­ба­ви­ли еще стоп-линию зе­ле­но­го цве­та (на­ри­суй­те ее в кон­це ла­би­рин­та) и зву­ки при со­уда­рении со стен­кой и успеш­ном про­хо­ж­дении ла­би­рин­та (рис. 3):

Рис. 3. Наш ро­бот те­перь су­ме­ет ос­та­но­вить­ся при дос­ти­же­нии кон­ца ла­би­рин­та.

По­экс­пе­ри­мен­ти­руй­те с раз­ны­ми ла­би­рин­та­ми и ал­го­рит­ма­ми.

Ус­ложним за­да­чу

Рис. 4. Но­вый ро­бот — чуть мень­ше, зато с дву­мя дат­чи­ка­ми.

Те­перь усложним на­ше­го ро­бо­та и по­ста­вим на него два дат­чи­ка – спра­ва и сле­ва по дви­жению, и пустим ро­бо­та ез­дить по по­лю с раз­бро­сан­ны­ми ку­би­ка­ми (рис. 4).

Так как у нас те­перь два дат­чи­ка ка­сания, то мы смо­жем точнее по­зи­циониро­вать ро­бо­та и оп­ре­де­лять на­хо­ж­дение пре­пят­ст­вий.

Но и ал­го­ритм ра­бо­ты так­же усложнит­ся:

1 Ро­бот дви­жет­ся впе­ред.

2 При сра­ба­ты­вании дат­чи­ка ка­сания ро­бот отъ­ез­жа­ет на­зад.

3 Ес­ли сра­бо­тал пра­вый дат­чик, то мы по­во­ра­чи­ва­ем­ся на неболь­шой угол (10 – 20 гра­ду­сов) вле­во.

4 Ес­ли сра­бо­тал ле­вый дат­чик, то мы по­во­ра­чи­ва­ем­ся впра­во.

5 Ес­ли сра­бо­та­ли оба дат­чи­ка, то мы по­во­ра­чи­ва­ем­ся впра­во на 45 гра­ду­сов.

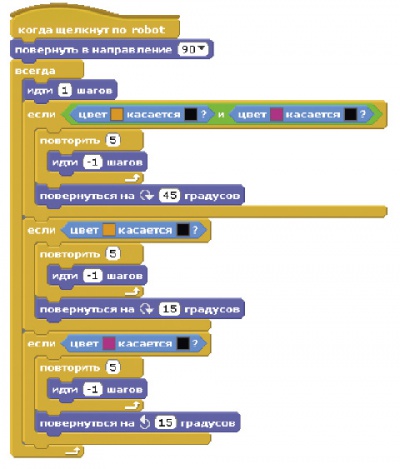
В бло­ках Scratch это бу­дет вы­гля­деть так:

За­пустив про­грам­му, вы че­рез неко­то­рое вре­мя мо­же­те столк­нуть­ся с тем, что ваш ро­бот уп­рет­ся в угол и не смо­жет из него вый­ти. Это свя­за­но с ог­раничением ал­го­рит­ма, ко­то­рый при пе­ре­мен­ном ка­сании дат­чи­ков по­во­ра­чи­ва­ет­ся на оп­ре­де­лен­ный угол то впра­во, то вле­во.

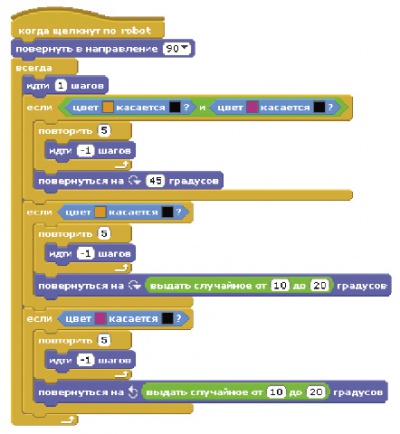
Вый­ти из по­ло­жения мож­но с по­мо­щью уве­ли­чения уг­ла по­во­ро­та при по­сле­до­ва­тель­ных ка­саниях или про­сто за­да­вая угол слу­чай­ным чис­лом (от 10 до 20 гра­ду­сов бу­дет доста­точ­но).

Тогда про­грам­ма при­мет сле­дую­щий вид:

Да бу­дет свет

Сле­дую­щий дат­чик, ко­то­рый мы рас­смот­рим и по­пы­та­ем­ся смо­де­ли­ро­вать, бу­дет дат­чи­ком осве­щения. В ре­аль­но­сти это обыч­но фо­то­ре­зи­стор или фо­то­тран­зи­стор, ко­то­рый, реа­ги­руя на уро­вень све­та, ме­ня­ет свою ха­рак­те­ри­сти­ку (к при­ме­ру, со­про­тив­ление). За счет пре­об­ра­зо­вания в Scratch бу­дет пе­ре­дан сиг­нал, ко­то­рый бу­дет из­ме­нять­ся от 0 до 100, где 0 – минималь­ный уро­вень осве­щения, 100 – мак­си­маль­ный.

Ис­точник све­та у нас бу­дет реа­ли­зо­ван в ви­де спрай­та ко­ну­са осве­щен­но­сти, ко­то­рый мож­но бу­дет пе­ре­дви­гать. Ро­бо­та мож­но взять из пер­во­го опы­та, раз­мес­тив ис­точник све­та по­се­ре­дине спе­ре­ди.

Рис. 5.

Ито­го­вое по­ле бу­дет вы­гля­деть, как показано на рис. 5.

Ал­го­ритм ра­бо­ты бу­дет та­кой:

1 По­сле вклю­чения ро­бот на­чи­на­ет кру­тить­ся на мес­те, ища ис­точник све­та.

2 Ес­ли он его на­хо­дит, то на­чи­на­ет полз­ти к нему.

3 Как толь­ко уро­вень сиг­на­ла па­да­ет, ро­бот опять на­чи­на­ет кру­тить­ся на мес­те.

А про­грам­ма по­лу­чит­ся та­кая:

Вы мо­же­те са­мо­стоя­тель­но до­ра­бо­тать про­грам­му и ис­поль­зо­вать два дат­чи­ка све­та, как и в слу­чае дат­чи­ков ка­сания. Так­же вы мо­же­те вве­сти пе­ре­мен­ную, чтобы смо­де­ли­ро­вать из­менение уров­ня осве­щен­но­сти при пе­ре­ме­щении от ис­точника или к нему. Это по­зво­лит ро­бо­ту дви­гать­ся в пра­виль­ном на­прав­лении, так как в те­ку­щем ал­го­рит­ме он дви­жет­ся толь­ко впе­ред и мо­жет уе­хать в об­рат­ном от ис­точника све­та на­прав­лении.

Что по­до мной

По­следний дат­чик, ко­то­рый мы рас­смот­рим в дан­ной ста­тье – дат­чик линии. По су­ти, это тот же дат­чик све­та, но ра­бо­таю­щий на от­ра­жение. Обыч­но дат­чик линии ра­бо­та­ет в неви­ди­мом ин­фра­крас­ном диа­па­зоне и по­зво­ля­ет оп­ре­де­лять, чер­ная или бе­лая по­верх­ность на­хо­дит­ся под ним.

Ал­го­ритм ра­бо­ты дат­чи­ка линии ана­ло­ги­чен дат­чи­ку ка­сания, с той разницей, что сиг­на­лом бу­дет не ка­сание стен­ки, а на­хо­ж­дение чер­ной линии, по ко­то­рой дол­жен дви­гать­ся ро­бот.

Рис. 6.

По­это­му возь­ми­те ис­ход­ные дан­ные от пер­во­го при­ме­ра, за­мените по­ле, по ко­то­ро­му бу­дет дви­гать­ся ро­бот, на по­ле с линией, и умень­ши­те раз­мер дат­чи­ка до неболь­шой точ­ки (рис. 6).

Те­перь мо­дернизи­руй­те ал­го­ритм. В слу­чае, когда ро­бот не на­хо­дит линию, он дол­жен вра­щать­ся. То есть усло­вие долж­но быть ин­верс­ным, и мы долж­ны толь­ко по­вер­нуть­ся на неболь­шой угол:

Увы, но наш ро­бот мо­жет дви­гать­ся толь­ко по линии, ко­то­рая име­ет пра­вые по­во­ро­ты. Для дви­жения по линии про­из­воль­ной фор­мы нуж­но ис­поль­зо­вать два дат­чи­ка, ко­то­рые по­зво­лят так­же оста­нав­ли­вать ро­бо­та на го­ри­зон­таль­ных чер­ных линиях.

Ви­до­из­мените ал­го­ритм са­мо­стоя­тель­но, ис­поль­зуя за осно­ву рас­смот­рен­ный ранее ал­го­ритм дви­жения ро­бо­та с дву­мя дат­чи­ка­ми ка­сания, и за­ставь­те ро­бо­та ез­дить по про­из­воль­но­му пу­ти.

На этом мы за­кон­чим наш мини-цикл. Вы мо­же­те уз­нать боль­ше об ро­бо­то­технике, ис­поль­зо­вании ре­аль­ных мик­ро­элек­трон­ных и ро­бо­то­техниче­­ских плат­форм Scratchduino, а так­же всю ин­фор­ма­цию, как са­мо­стоя­тель­но по­стро­ить их, ме­то­ди­ку обу­чения и мно­гое дру­гое на ви­ки про­ек­та Edumandriva по ад­ре­су http://edumandriva.ru/wiki/index.php/ScratchDuino. |