LXF107:SciLab
(викификация, оформление, иллюстрация, формула) |
Yaleks (обсуждение | вклад) м (→Отладка) |
||
| Строка 308: | Строка 308: | ||
Конечно же, рамки статьи не позволяют мне описать все, что хотелось бы, особенно это касается программирования. Но я надеюсь, что | Конечно же, рамки статьи не позволяют мне описать все, что хотелось бы, особенно это касается программирования. Но я надеюсь, что | ||
| − | данная статья даст вам некоторое представление о возможностях и принципах работы ''SciLab'' с функциями. Если вас заинтересовала эта тема, напишите нам на | + | данная статья даст вам некоторое представление о возможностях и принципах работы ''SciLab'' с функциями. Если вас заинтересовала эта тема, напишите нам на [mailto:letters@linuxformat.ru letters@linuxformat.ru] – возможно, мы выпустим несколько уроков по программированию в ''SciLab''. '''LXF''' |
===Форматируем график=== | ===Форматируем график=== | ||
Версия 16:20, 24 августа 2009
|
|
|
- SciLab Лаборатория численных расчетов, открытая для всех желающих
- Метамодернизм в позднем творчестве В.Г. Сорокина
- ЛитРПГ - последняя отрыжка постмодерна
- "Ричард III и семиотика"
- 3D-визуализация обложки Ridero создаем обложку книги при работе над самиздатом.
- Архитектура метамодерна - говоря о современном искусстве, невозможно не поговорить об архитектуре. В данной статье будет отмечено несколько интересных принципов, характерных для построек "новой волны", столь притягательных и скандальных.
- Литература
- Метамодерн
- Рокер-Прометей против изначального зла в «Песне про советскую милицию» Вени Дркина, Автор: Нина Ищенко, к.ф.н, член Союза Писателей ЛНР - перепубликация из журнала "Топос".
- Как избавиться от комаров? Лучшие типы ловушек.
- Что делать если роблокс вылетает на windows
- Что делать, если ребенок смотрит порно?
- Почему собака прыгает на людей при встрече?
- Какое масло лить в Задний дифференциал (мост) Visco diff 38434AA050
- О чем может рассказать хвост вашей кошки?
- Верветки
- Отчетность бюджетных учреждений при закупках по Закону № 223-ФЗ
- Срок исковой давности как правильно рассчитать
- Дмитрий Патрушев минсельхоз будет ли преемником Путина
- Кто такой Владислав Поздняков? Что такое "Мужское Государство" и почему его признали экстремистским в России?
- Как правильно выбрать машинное масло в Димитровграде?
- Как стать богатым и знаменитым в России?
- Почему фильм "Пипец" (Kick-Ass) стал популярен по всему миру?
- Как стать мудрецом?
- Как правильно установить FreeBSD
- Как стать таким как Путин?
- Где лучше жить - в Димитровграде или в Ульяновске?
- Почему город Димитровград так называется?
- Что такое метамодерн?
- ВАЖНО! Временное ограничение движения автотранспортных средств в Димитровграде
- Тарифы на электроэнергию для майнеров предложено повысить
Содержание |
Функции: встроенные и внешние
- ЧАСТЬ 2 Какая же математика без функций? Александр Бикмеев покажет, что может предложить здесь SciLab, на примере задачи о теле, брошенном под углом к горизонту.
На прошлом занятии мы узнали, что такое SciLab, поработали с матрицами, решили систему уравнений и построили графики. Теперь настало время копнуть чуть глубже, ведь все эти действия можно выполнить и в OOo Calc.
Inline-функции
SciLab имеет большую библиотеку встроенных функций, однако вряд ли разработчики включили в нее ту самую, которую необходимо проанализировать вам: например, описывающую перемещение тела, брошенного под углом к горизонту. Ею мы и займемся на данном уроке. Пусть движение тела по оси Oy описывает изменение высоты над поверхностью земли, а по оси Ox – дальность полета. Соответствующие функции имеют вид:
<math>h(t)=h_0 + v_0 sin(\alpha) t - \frac{gt^2}{2}</math>
<math>s(t)=s_0 + v_0 cos(\alpha) t \frac{}{}</math>
где – <math>v_0</math> модуль вектора начальной скорости, <math>h_0</math> и <math>s_0</math> – начальная высота и смещение от точек отсчета по вертикали и горизонтали, соответственно, – α угол между вектором начальной скорости и горизонтом.
Эти функции довольно просты, поэтому можно, конечно, вводить их в виде отдельных выражений всякий раз, когда это потребуется. Мы, однако, пойдем другим путем и запишем их в виде так называемых inline-функций, т.е. функций, описываемых в одну команду.
Пусть тело сброшено с высоты 2 км. Вот как можно узнать, на какой высоте оно окажется спустя 5, 10, 15 и 20 секунд.
-->deff('[y]=h(t)','y=h0+v0*sin(alpha)*t-g*t^2/2');
-->deff('[x]=s(t)','x=s0+v0*cos(alpha)*t');
-->h0=2000;alpha=(-90*%pi/180);v0=0;g=9.81;
-->t=[5,10,15,20];
-->h(t)
ans =
1877.375 1509.5 896.375 38.
Значение угла (<math>-90^o</math>) необходимо перевести в радианы: SciLab, как и многие системы, использует именно их. Если вы твердо хотите работать с градусами, то можете переопределить h(t) и s(t) следующим образом:
-->deff('[y]=h(t)','y=h0+v0*sin(alpha*%pi/180)*t-g*t^2/2');
-->deff('[x]=s(t)','x=s0+v0*cos(alpha*%pi/180)*t');
Поскольку любая функция – это, практически, переменная, то и вычисляться она будет в соответствии с описанием, заданным последним. Однако мы далее будем работать с радианами, то есть с первой версией функций.
Подобным образом можно описать любые некусочно заданные функции. Общий вид таков:
deff('[<результат> = <имя функции>(<входные переменные>)]','<мат.описание функции>','ключ')
Ключ – необязательный параметр, принимающий значения c или n. В первом случае функция будет скомпилирована, что повышает быстродействие, а во втором – нет; по умолчанию действует ключ c. Однако не следует считать, что inline-функции годятся только для простых случаев. Математическое описание функции, а также результат, могут представлять собой матрицу и содержать многошаговые вычисления. Возьмем, например, функцию Qroots(), решающую квадратные уравнения:
-->deff('[x1, x2]=Qroots(Qa,Qb,Qc)',['D=Qb^2-4*Qa*Qc';'x1=(-Qb+sqrt(D))/(2*Qa)';'x2=(-Qb-sqrt(D))/(2*Qa)']);
Опробуем ее на нашем примере. Пусть начальная высота равна нулю, а скорость равна 20 м/с и направлена вверх (<math>90^o</math>). Определим, когда тело окажется на высоте 20 м. Если ось Oy направлена вертикально вверх, то уравнение будет иметь вид:
<math>20 - 20t + \frac {9,81t^2}{2} = 0</math>
Найдем его корни при помощи Qroots:
-->[h1,h2] = Qroots(9.81/2,-20,20)
h2 =
1.7577156
h1 =
2.3197563
Решим уравнение с другими коэффициентами:
-->[q1,q2]=Qroots(1,2,3) q2 = - 1. - 1.4142136i q1 = - 1. + 1.4142136i
Как видно из этого примера, в тексте описания функции можно создавать внутренние переменные. И кроме того, нам не пришлось обрабатывать случай отрицательного дискриминанта, поскольку SciLab понимает мнимые числа и умеет работать с ними. Впрочем, он также умеет решать алгебраические и трансцендентные уравнения и без нашей помощи, так что вернемся к примеру с бросанием.
- Метамодернизм в позднем творчестве В.Г. Сорокина
- ЛитРПГ - последняя отрыжка постмодерна
- "Ричард III и семиотика"
- 3D-визуализация обложки Ridero создаем обложку книги при работе над самиздатом.
- Архитектура метамодерна - говоря о современном искусстве, невозможно не поговорить об архитектуре. В данной статье будет отмечено несколько интересных принципов, характерных для построек "новой волны", столь притягательных и скандальных.
- Литература
- Метамодерн
- Рокер-Прометей против изначального зла в «Песне про советскую милицию» Вени Дркина, Автор: Нина Ищенко, к.ф.н, член Союза Писателей ЛНР - перепубликация из журнала "Топос".
- Как избавиться от комаров? Лучшие типы ловушек.
- Что делать если роблокс вылетает на windows
- Что делать, если ребенок смотрит порно?
- Почему собака прыгает на людей при встрече?
- Какое масло лить в Задний дифференциал (мост) Visco diff 38434AA050
- О чем может рассказать хвост вашей кошки?
- Верветки
- Отчетность бюджетных учреждений при закупках по Закону № 223-ФЗ
- Срок исковой давности как правильно рассчитать
- Дмитрий Патрушев минсельхоз будет ли преемником Путина
- Кто такой Владислав Поздняков? Что такое "Мужское Государство" и почему его признали экстремистским в России?
- Как правильно выбрать машинное масло в Димитровграде?
- Как стать богатым и знаменитым в России?
- Почему фильм "Пипец" (Kick-Ass) стал популярен по всему миру?
- Как стать мудрецом?
- Как правильно установить FreeBSD
- Как стать таким как Путин?
- Где лучше жить - в Димитровграде или в Ульяновске?
- Почему город Димитровград так называется?
- Что такое метамодерн?
- ВАЖНО! Временное ограничение движения автотранспортных средств в Димитровграде
- Тарифы на электроэнергию для майнеров предложено повысить
Давайте построим траекторию полета тела в течение первых 10 секунд при начальной скорости 20 м/с и угле <math>90^o</math>, считая, что <math>h_0 = s_0 = 0</math>. Для этого нам необходимо создать вектор значений времени (t), а затем построить график, где по оси Ox будет отложена s(t), а по оси Oy – h(t):
-->h0=0;s0=0;alpha=(45*%pi/180);v0=20;g=9.81; -->t=0:0.1:10; -->plot(s(t),h(t),'r-')
В результате мы получили траекторию полета тела, которая представляет собой график функции h(s), заданной параметрически. Прочитавшие наш урок в LXF106, вероятно, обратят внимание на добавку r- в вызове plot(). Это специальный параметр, регулирующий оформление. Видите, линия на рис. 1 не черная, а красная? Остальные значения приведены во врезке Форматируем график.
Итак, наше тело ушло в недра земли. Чтобы этого не случилось, мы должны грамотно задавать диапазон расчета, т.е. определить, где высота становится равной нулю. Элегантное решение мы разработаем чуть позднее, а пока воспользуемся встроенными средствами.
Функция fsolve позволяет решать линейные и нелинейные уравнения, а также их системы, заданные функциями, то есть находить нули функций. Поскольку ищется численное, а не аналитическое решение, то в результате мы получим одно число. Однако какое решение мы найдем, зависит от значения начального приближения. Так происходит потому, что, как правило, методы численного решения алгебраических уравнений позволяют найти ближайший к указанной точке корень.
Общий вид вызова функции таков:
eqAns = fsolve(vInit,F,Fj,e)
где eqAns – это переменная или вектор решений, vInit – начальное значение или вектор начальных значений, F – функция или список функций, представляющих собой левые части уравнений, Fj – это производная или список производных функций F, e – точность. Последние два параметра необязательны.
Чтобы корректно построить траекторию, нам необходимо найти нетривиальный положительный корень уравнения h(t) = 0. Зададим начальное приближение, равное 5.
-->t_end=fsolve(5,h) t_end = 2.8832081 -->t=0:0.01:t_end; -->plot(s(t),h(t),'r-')
Выполните эти команды самостоятельно и посмотрите результат.
Полиномы
Конечно, искать корни по одному – это неплохо, но как быть, если необходимо узнать их оба сразу? Здесь поможет другой подход, не использующий inline-функций. Если внимательно посмотреть на h(t), то можно заметить, что она представляет собой полином второй степени относительно t. В SciLab встроено достаточно инструментов для работы с полиномами – в частности, есть функция root, возвращающая их корни.
Перед использованием полином необходимо определить. Делается это при помощи функции poly. Ее первый аргумент – это вектор-строка коэффициентов или корней полинома (смысл определяется флагом), второй – символьная переменная, а третий – флаг, принимающий значения roots или coeff. Например, пусть нам известно, что начальная высота полета равна 10 м, начальная скорость – 10 м/с и угол равен <math>300^o</math>. Требуется записать закон изменения высоты со временем.
-->hCoeff = [10, 10*sin(30*%pi/180),-9.81/2]; -->h=poly(hCoeff,'t','coeff') h= 10 + 5t - 4.905t2
Здесь мы указали флаг coeff, сообщающий, что первый параметр – это вектор коэффициентов полинома. А теперь определим, сколько секунд тело уже находится в полете и когда оно упадет на землю.
-->roots(h)
ans =
- 1.006401
2.025769
То есть тело было брошено примерно секунду назад и упадет примерно через две секунды.
Теперь попробуем пойти другим путем. Известно, что тело находится в полете 3 секунды и через 5 секунд упадет на землю. Определить закон изменения высоты.
-->hRoots = [-3,5];
-->h=poly(hRoots,'t','roots')*(-9.81)/2
h=
73.575 + 9.81t – 4.905t2
Таким образом, в настоящий момент времени тело находится на высоте 73,5 метра и имеет вертикальную скорость, равную 9,81 м/с. В данном случае флаг roots (используется по умолчанию) означает, что первый параметр – это корни полинома, который следует сформировать.
Естественно, работа с полиномами не ограничивается этими двумя функциями. В версии 4.1.2 их насчитывается более 35, среди которых нахождение эрмитовой формы (hermit), полиномиальное деление (pdiv), рациональное упрощение (simp) и многое другое – посмотрите раздел Polinomial calculations в справке. Кроме того, с полиномами можно работать так же, как с обычными переменными, то есть вычитать, умножать, возводить в степень и т.д. при помощи символов обычных арифметических действий. Например, определим два полинома, а затем выполним с ними все четыре арифметических действия, а также возведем один из них в квадрат.
-->p1=poly([27,0,0,-8],'s','coeff')
p1 =
27 - 8s3
-->p2=poly([9,6,4],'s','coeff')
p2 =
9 + 6s + 4s2
-->p_add=p1+p2
p_add =
36 + 6s + 4s2 - 8s3
-->p_decr=p1-p2
p_decr =
18 - 6s - 4s2 - 8s3
-->p_div=p1/p2
p_div =
3 - 2s
------
1
-->p_mult=p1*p2
p_mult =
243 + 162s + 108s2 - 72s3 - 48s4 - 32s5
-->p_degr=p2^2
p_degr =
81 + 108s + 108s2 + 48s3 + 16s4
Внешние функции
Да, возможности SciLab достаточно обширны, хотя их пока все-таки нельзя сравнивать с функционалом Matlab; и все же у этих двух программ есть нечто общее – их часто называют системами разработки высокотехнологичных приложений. А это значит, что у SciLab (как и MatLab) есть встроенный язык программирования. На самом деле, все функции, которые мы использовали, также входят в этот язык, наряду с обычными конструкциями (условие, цикл) и возможностями использования графики. Следовательно, программист, работая в SciLab, может не отвлекаться на реализацию численных методов, а использовать уже готовые наработки.
- Метамодернизм в позднем творчестве В.Г. Сорокина
- ЛитРПГ - последняя отрыжка постмодерна
- "Ричард III и семиотика"
- 3D-визуализация обложки Ridero создаем обложку книги при работе над самиздатом.
- Архитектура метамодерна - говоря о современном искусстве, невозможно не поговорить об архитектуре. В данной статье будет отмечено несколько интересных принципов, характерных для построек "новой волны", столь притягательных и скандальных.
- Литература
- Метамодерн
- Рокер-Прометей против изначального зла в «Песне про советскую милицию» Вени Дркина, Автор: Нина Ищенко, к.ф.н, член Союза Писателей ЛНР - перепубликация из журнала "Топос".
- Как избавиться от комаров? Лучшие типы ловушек.
- Что делать если роблокс вылетает на windows
- Что делать, если ребенок смотрит порно?
- Почему собака прыгает на людей при встрече?
- Какое масло лить в Задний дифференциал (мост) Visco diff 38434AA050
- О чем может рассказать хвост вашей кошки?
- Верветки
- Отчетность бюджетных учреждений при закупках по Закону № 223-ФЗ
- Срок исковой давности как правильно рассчитать
- Дмитрий Патрушев минсельхоз будет ли преемником Путина
- Кто такой Владислав Поздняков? Что такое "Мужское Государство" и почему его признали экстремистским в России?
- Как правильно выбрать машинное масло в Димитровграде?
- Как стать богатым и знаменитым в России?
- Почему фильм "Пипец" (Kick-Ass) стал популярен по всему миру?
- Как стать мудрецом?
- Как правильно установить FreeBSD
- Как стать таким как Путин?
- Где лучше жить - в Димитровграде или в Ульяновске?
- Почему город Димитровград так называется?
- Что такое метамодерн?
- ВАЖНО! Временное ограничение движения автотранспортных средств в Димитровграде
- Тарифы на электроэнергию для майнеров предложено повысить
Как и любая среда разработки, SciLab обладает текстовым редактором с подсветкой синтаксиса – SciPad. Вызывается он выбором пункта меню Editor или командой editor. Редактор, в отличие от оболочки SciLab, способен отображать комментарии, набранные кириллицей, однако русского интерфейса не имеет. Вот здесь вы и можете поучаствовать в проекте, поскольку перевод выполняется достаточно просто, а файл не так уж велик. Описание того, как сделать перевод, можно вызвать из SciPad (Help > Adding translation...) Желающие – вперед!
Интерфейс предельно прост: строка текстового меню, а под ней рабочая область. Вот в меню-то и сосредоточена вся сила SciPad; кроме того, почти все его команды имеют «горячие» клавиши. Пункты меню достаточно стандартны, но хочется отметить, что этот редактор имеет средства отладки (пункт меню Debug), настраиваемую подсветку синтаксиса, проверку парности скобок и прямую выгрузку результата в SciLab на выполнение.
При помощи текстового редактора SciPad мы сможем создать более элегантное решение для расчета дальности полета тела, брошенного под углом к горизонту (о чем упоминалось ранее). А именно, мы напишем внешнюю функцию, которую можно будет подгружать во время работы и пользоваться ею так же, как и встроенными. Кстати, именно так и выполнены все расширения и многие встроенные функции системы SciLab. Чтобы убедиться в этом, откройте каталог, куда был установлен SciLab. Если вы используете двоичную версию с LXFDVD, то это папка, в которую вы распаковали архив; если же вы устанавливали программу через менеджер пакетов вашей системы, то поищите в /usr/lib каталог с именем scilab-4.1.2, в моем дистрибутиве (Mandriva 2008.1) он располагается именно там. Затем перейдите в каталог macros, и вы увидите множество каталогов, имена которых напоминают названия блоков функций в справке (elem – Elementary Function, optim – Optimisation and simulation и так далее). Внутри них находятся файлы с расширениями .bin и .sci: первые – это откомпилированные версии функций, а вторые – исходные тексты. Я рекомендую всем покопаться здесь, поскольку именно так, в отсутствие справочных материалов, можно не только досконально изучить принципы создания приложений в SciLab, но и выяснить причины возникновения ошибок при использовании стандартных функций. Может оказаться, что реализованный разработчиками метод (все мы не без греха) неэффективен или содержит ошибку, тогда вы сможете его исправить. Кроме того, настоятельно рекомендую посмотреть содержимое каталога /usr/lib/scilab-4.1.2/demos, в котором находятся исходные тексты всех демонстрационных примеров.
Вернемся к нашей задаче. Полный текст функции приведен на рис. 2. Первые строки, начинающиеся с двойного слэша (//) – это комментарии. Затем идет заголовок функции:
function [<список выходных параметров>] = <Имя Функции>(<список входных параметров>) <тело функции> endfunction
В дальнейшем именно Имя функции и будет использоваться в окне SciLab. Все остальное является локальным содержимым и на рабочую среду оказывать влияния не будет. Следует отметить, что если при определении функции не указаны выходные параметры, то есть функция ничего не возвращает, то она будет являться процедурой. Как правило, в виде процедур оформляются такие участки программы, как отрисовка графика или картинки, ввод и проверка данных и т.д.
В следующих двух строках мы определяем значение ускорения свободного падения и переводим угол из градусов в радианы. Далее, поскольку мы будем использовать функцию fsolve, задается начальное приближение и устанавливается значение времени, равное нулю. Как уже говорилось ранее, fsolve ищет решение, ближайшее к начальному приближению, поэтому его необходимо задать так, чтобы найденное время было больше нуля. Для этого мы увеличиваем начальное приближение (переменная Init_t) на 10 в цикле до тех пор, пока найденное решение (переменная t) не станет положительным. Таким образом мы сможем найти момент, когда тело упадет на землю. А затем, по формуле для равномерного движения, мы вычисляем, какое расстояние пройдет тело за это время вдоль горизонтальной оси.
Результаты вычисления заносятся в переменные, являющиеся выходными параметрами. В нашем случае он один – s. На этом выполнение функции заканчивается, и результат передается на выход. Теперь нам осталось записать функцию в файл. Для этого выберите последовательно пункты меню File > Save as... или воспользуйтесь комбинацией клавиш Ctrl+Shift+S и сохраните файл в своем домашнем каталоге под именем flyrange.sci.
В следующий раз, когда нам понадобится эта функция, мы сможем подключить ее при помощи процедуры getf, которая принимает полный путь и название файла функции. Предположим, что вы (firstuser) сохранили файл в своем домашнем каталоге. Тогда команда будет такой:
getf /home/firstuser/flyrange.sci
После ее выполнения вы сможете использовать вашу собственную функцию в вычислениях. Кроме того, функцию можно загрузить в SciLab непосредственно из редактора SciPad, для чего необходимо последовательно выбрать пункты меню Execute > Load into Scilab или нажать комбинацию клавиш Ctrl+Shift+I. После этого весь исходный код будет передан в SciLab и выполнен. Если вы создали в редакторе не функцию, а просто последовательность команд, она будет выполнена, а результат – выведен на экран.
Конечно, лучше было бы самостоятельно реализовать численный метод решения уравнения, но выбранный нами подход позволяет получить компактный код, а также демонстрирует возможность использования встроенных функций при разработке программ.
Отладка
- Метамодернизм в позднем творчестве В.Г. Сорокина
- ЛитРПГ - последняя отрыжка постмодерна
- "Ричард III и семиотика"
- 3D-визуализация обложки Ridero создаем обложку книги при работе над самиздатом.
- Архитектура метамодерна - говоря о современном искусстве, невозможно не поговорить об архитектуре. В данной статье будет отмечено несколько интересных принципов, характерных для построек "новой волны", столь притягательных и скандальных.
- Литература
- Метамодерн
- Рокер-Прометей против изначального зла в «Песне про советскую милицию» Вени Дркина, Автор: Нина Ищенко, к.ф.н, член Союза Писателей ЛНР - перепубликация из журнала "Топос".
- Как избавиться от комаров? Лучшие типы ловушек.
- Что делать если роблокс вылетает на windows
- Что делать, если ребенок смотрит порно?
- Почему собака прыгает на людей при встрече?
- Какое масло лить в Задний дифференциал (мост) Visco diff 38434AA050
- О чем может рассказать хвост вашей кошки?
- Верветки
- Отчетность бюджетных учреждений при закупках по Закону № 223-ФЗ
- Срок исковой давности как правильно рассчитать
- Дмитрий Патрушев минсельхоз будет ли преемником Путина
- Кто такой Владислав Поздняков? Что такое "Мужское Государство" и почему его признали экстремистским в России?
- Как правильно выбрать машинное масло в Димитровграде?
- Как стать богатым и знаменитым в России?
- Почему фильм "Пипец" (Kick-Ass) стал популярен по всему миру?
- Как стать мудрецом?
- Как правильно установить FreeBSD
- Как стать таким как Путин?
- Где лучше жить - в Димитровграде или в Ульяновске?
- Почему город Димитровград так называется?
- Что такое метамодерн?
- ВАЖНО! Временное ограничение движения автотранспортных средств в Димитровграде
- Тарифы на электроэнергию для майнеров предложено повысить
Если при создании вашей собственной функции или процедуры у вас возникли трудности: неверный результат, ошибка при вычислении или что-то еще, то вы всегда можете выполнить программу в режиме пошаговой отладки.
Прежде чем перейти в режим отладки, вам следует определить значения входных параметров, поскольку в противном случае функция не сможет работать. Для этого либо последовательно выбираем пункты меню Debug > Configure Execution..., либо нажимаем клавишу F10. В данном случае появится окно, показанное на рис. 3. В верхней строчке вы можете указать функцию, из которой следует брать входные параметры (если таковая имеется), и нажать кнопку Obtain. Если же входные параметры должны вводиться пользователем, придется указать их вручную. Для этого следует выбрать переменную из списка и нажать кнопку Add/Change. В появившемся окне, в первой строке отображается имя переменной, а во второй – вводится ее значение. Кроме того, если какой-либо переменной нет в списке, вы можете добавить ее, просто изменив имя в первой строке. Нажатие второй кнопки (Remove) приводит к удалению выделенной в данный момент переменной.
- Метамодернизм в позднем творчестве В.Г. Сорокина
- ЛитРПГ - последняя отрыжка постмодерна
- "Ричард III и семиотика"
- 3D-визуализация обложки Ridero создаем обложку книги при работе над самиздатом.
- Архитектура метамодерна - говоря о современном искусстве, невозможно не поговорить об архитектуре. В данной статье будет отмечено несколько интересных принципов, характерных для построек "новой волны", столь притягательных и скандальных.
- Литература
- Метамодерн
- Рокер-Прометей против изначального зла в «Песне про советскую милицию» Вени Дркина, Автор: Нина Ищенко, к.ф.н, член Союза Писателей ЛНР - перепубликация из журнала "Топос".
- Как избавиться от комаров? Лучшие типы ловушек.
- Что делать если роблокс вылетает на windows
- Что делать, если ребенок смотрит порно?
- Почему собака прыгает на людей при встрече?
- Какое масло лить в Задний дифференциал (мост) Visco diff 38434AA050
- О чем может рассказать хвост вашей кошки?
- Верветки
- Отчетность бюджетных учреждений при закупках по Закону № 223-ФЗ
- Срок исковой давности как правильно рассчитать
- Дмитрий Патрушев минсельхоз будет ли преемником Путина
- Кто такой Владислав Поздняков? Что такое "Мужское Государство" и почему его признали экстремистским в России?
- Как правильно выбрать машинное масло в Димитровграде?
- Как стать богатым и знаменитым в России?
- Почему фильм "Пипец" (Kick-Ass) стал популярен по всему миру?
- Как стать мудрецом?
- Как правильно установить FreeBSD
- Как стать таким как Путин?
- Где лучше жить - в Димитровграде или в Ульяновске?
- Почему город Димитровград так называется?
- Что такое метамодерн?
- ВАЖНО! Временное ограничение движения автотранспортных средств в Димитровграде
- Тарифы на электроэнергию для майнеров предложено повысить
Итак, пусть входные параметры определены. Нажмите кнопку OK и закройте это окно. Теперь, если вы вновь выберете пункт меню Debug, то увидите, что практически все пункты меню стали активны. Вы можете установить/убрать точку останова в текущей строке (F9), удалить все точки останова (Ctrl+F9), выполнить до курсора (Ctrl+F11) и так далее. Пошаговое перемещение выполняется при помощи клавиш F8 (без захода в подпрограммы) Shift+F8 (с заходом в подпрограммы). В ходе выполнения программы вы также можете просматривать значения локальных переменных. Для этого следует вывести на экран окно наблюдения (Watch), нажав Ctrl+F12 или Debug > Show watch. Окно наблюдения содержит три области (рис. 4):
- верхняя – для наблюдения за значениями переменных. При помощи кнопки Add/change вы можете добавлять и изменять переменные. Кроме того, здесь есть две очень полезные опции: Auto (local variables) и Auto watch globals too. Выбор первой позволяет автоматически перенести в окно наблюдения все локальные переменные, а второй – глобальные. Как видно из рис. 4, последнее вычисленное значение отображается красным цветом.
- срединная область для проведения вычислений с текущими значениями переменных.
- нижняя область для отображения стека вызовов.
Таким образом, вы можете полностью контролировать процесс выполнения.
Конечно же, рамки статьи не позволяют мне описать все, что хотелось бы, особенно это касается программирования. Но я надеюсь, что данная статья даст вам некоторое представление о возможностях и принципах работы SciLab с функциями. Если вас заинтересовала эта тема, напишите нам на letters@linuxformat.ru – возможно, мы выпустим несколько уроков по программированию в SciLab. LXF
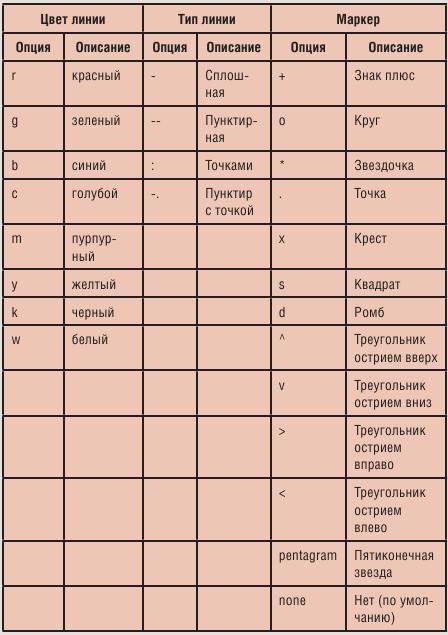
Форматируем график
Опции форматирования линии двумерного графика в SciLab разбиты на три категории: цвет линии, тип линии, маркер значения. Они указываются в функции plot в кавычках в любом порядке после массивов с данными для построения. Ниже приведена таблица с описанием каждого из параметров.