Журнал LinuxFormat - перейти на главную

LXF78:MetaPost

Материал из Linuxformat
Перейти к: навигация, поиск
Подписка на печатную версию
Весь 2015 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)
Подписка на электронную версию
Весь 2015 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)
Подшивки старых номеров журнала (печатные версии)
Весь 2014 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)

Часть 3. Компьютер не умеет читать ваши мысли, зато неукоснительно следует инструкциям. Евгений Балдин научит вас отдавать правильные команды и извлекать из этого выгоду.

До сего момента мы концентрировались на том, как объяснить компьютеру, чтобы он сделал то или иное движение. Теперь воспользуемся способностью компьютера помнить предыдущие действия и извлекать их из памяти по мере необходимости. Автоматизация рутинных процедур это то, для чего компьютеры и предназначены. Практиковаться в автоматизации следует постоянно. Несмотря на затраченное на обучение время, в результате время же и экономится.

Содержание

Объекты picture

В процесс повествования объект picture или картинка уже упоминался. Картинка представляет из себя совокупность путей и точек, которую можно подвергать трансформации. В уже существующие картинки можно добавлять пути, замкнутые области и другие картинки.

Для начала опять же воспользуемся миллиметровкой для отрисовки какого-либо рисунка, например, ракеты:
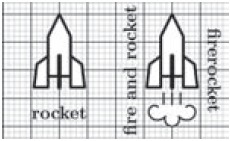
Img 78 104 1.jpg

Ракета может быть без выхлопа (rocket) и c выхлопом (firerocket). В процессе создания firerocket был использован рисунок самого выхлопа (fire). 

%Файл picture.1.mp
%Ракета без выхлопа 10x12 Центр у стабилизаторов
 picture rocket;rocket:=nullpicture;
 addto rocket contour (-2,-1)--(-2,6)--(0,10)--(2,6)--(2,-1)--cycle
 withpen pencircle scaled 0.4 withcolor white;
 addto rocket  doublepath (-2,-1)--(-2,6)--(0,10)--(2,6)--(2,-1)--cycle
 withpen pencircle scaled 0.5;%Корпус
 addto rocket contour (-2,2.5)--(-4,1)--(-4.5,-3)--(-2,-3)--cycle
 withpen pencircle scaled 0.4 withcolor white;
 addto rocket  doublepath (-2,2.5)--(-4,1)--(-4.5,-3)--(-2,-3)--cycle
 withpen pencircle scaled 0.5;%левая дюза
 addto rocket contour (2,2.5)--(4,1)--(4.5,-3)--(2,-3)--cycle
 withpen pencircle scaled 0.4 withcolor white;
 addto rocket  doublepath (2,2.5)--(4,1)--(4.5,-3)--(2,-3)--cycle
 withpen pencircle scaled 0.5;%правая дюза
 addto rocket  doublepath (0,2.5)--(0,-3)
 withpen pencircle scaled 0.8;%центральная дюза
 %выхлоп
 picture fire;fire:=nullpicture;
 addto fire  doublepath (0,-4)--(0,-6)
 withpen pencircle scaled 0.3;%выхлоп 1
 addto fire  doublepath (-1.5,-4)--(-1.5,-6)
 withpen pencircle scaled 0.3;%выхлоп 2
 addto fire  doublepath (1.5,-4)--(1.5,-6)
 withpen pencircle scaled 0.3;%выхлоп 3
 addto fire  contour (-2.5,-6.5){dir 135}..(-4,-8)..
 {dir 50}(-1.2,-8.2){dir -110}..(0,-10)
 ..{dir 110}(1.2,-8.2){dir -50}..(4,-8)..{dir -135}(2.5,-6.5)--cycle
 withpen pencircle scaled 0.4 withcolor white;
 addto fire  doublepath (-2.5,-6.5){dir 135}..(-4,-8)..
 {dir 50}(-1.2,-8.2){dir -110}..(0,-10)
 ..{dir 110}(1.2,-8.2){dir -50}..(4,-8)..{dir -135}(2.5,-6.5)
 withpen pencircle scaled 0.3;%облако
 %ракета и выхлоп
 picture firerocket;firerocket:=rocket;
 addto firerocket also fire;

Прежде чем что-то добавить к картинке, её необходимо инициализировать. В MetaPost есть две определённые по умолчанию картинки: nullpicture — пустая картинка и currentpicture — текущая картинка. Пользуясь последней переменной, можно в любой момент сохранить результаты промежуточной отрисовки. Добавление элементов к картинке производится с помощью инструкции addto, после которой указывается картинка, к которой и добавляется тот или иной элемент. Путь добавляется с помощью инструкции doublepath, замкнутая область — с помощью инструкции contour, а другая картинка с помощью инструкции also.

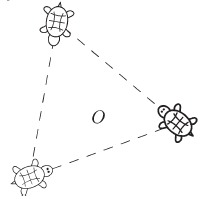
Ранее был создан рисунок черепашки. Для его обозначения была выбрана переменная Turtle. Теперь с ней можно поработать, как с единым элементом, например, для иллюстрации задачи: «Черепашки расположены в углах правильного треугольника со стороной a и всегда ползут в направлении своей соседки против часовой стрелки со скоростью v. Когда они встретятся?»


Img 78 105 1.jpg

Картинку можно отобразить с помощью команды draw. Над картинкой можно производить различные преобразования. В данном случае картинка поворачивалась, масштабировалась и сдвигалась. 

%Файл pic.mp
beginfig(17) ;
numeric u;u = 0.8mm;
numeric dphi; dphi=20;
   draw 30u*dir (90+dphi)--30u*dir (210+dphi)--30u*dir (330+dphi)--cycle 
   dashed evenly scaled 1u;
   draw Turtle rotated (-120+dphi) scaled 1u shifted (30u*dir (90+dphi));
   draw Turtle rotated dphi scaled 1u shifted (30u*dir (210+dphi));
   draw Turtle rotated (120+dphi) scaled 1u shifted (30u*dir (330+dphi));
endfig ;

Обратите внимание, что линия, соединяющая черепах, нарисована пунктиром. Определённая по умолчанию переменная evenly тоже является картинкой, поэтому её можно масштабировать с помощью декларации scaled. То есть, если вам нужен более широкий шаг пунктира, то вместо масштаба 1u можно указать 2u. Если вас не устраивает где располагаются штрихи у штриховки, то можно воспользоваться декларацией сдвига shifted.

Кроме шаблона evenly в MetaPost определён шаблон withdots, который позволяет рисовать кривую с помощью точек.

Вы можете определить свой шаблон для пунктира примерно следующим образом: 

picture dash_center;
dash_center:=dashpattern(on 3 off 1.5 on 0.5 off 1.5);
draw 30u*dir (90+dphi)--30u*dir (210+dphi)--  30u*dir (330+dphi)--cycle dashed dash_center scaled 1u;

Функция dashpattern принимает список on/off с числовой информацией в какой момент рисовать/не рисовать. В этом примере определён шаблон для штрих-пунктирной линии, которая обычно используется для обозначения оси симметрии.

Трансформация

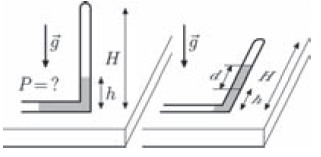
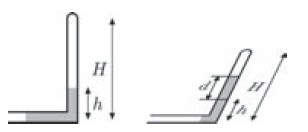
К задаче N 3 варианта ГГФ-51в требовалось изобразить L-образную трубку с водой. По условию, трубка сначала стояла вертикально, а потом была положена на стол.

Чтобы схематично это изобразить, вовсе необязательно уметь работать в трёхмерном редакторе. Ниже идёт код, который рисует вертикально стоящую пробирку с размерами, а затем наклоняет её.


Img 78 105 3.jpg 

%Файл transform.mp
%пример использования slanted
beginfig(1) ;
numeric u;
u = 0.8mm;
%пробирка
cutdraw (0u,0u)--(20u,0u)--(20u,30u){dir 90}..
 {dir -90}(17u,30u)--(17u,3u)--(0u,3u)
 withpen pencircle scaled 0.5u;
drawdblarrow (23u,10u)--(23u,1u);
label.rt(btex \(h\) etex,1/2[(23u,10u),(23u,1u)]);
drawdblarrow (30u,30u)--(30u,1u);
label.lft(btex \(H\) etex,1/2[(30u,30u),(30u,1u)]);
picture Base;
Base:=currentpicture; %запоминаем
clearit; %очищаем текущую картинку
%рисуем воду когда пробирка будет наклонена
fill (15u,0u)--(20u,0u)--(20u,20u)--(17u,20u)--
 (17u,3u)--(15u,3u)--cycle withcolor 0.7white;
draw Base;
draw (12u,20u)--(20u,20u);draw (12u,10u)--(20u,10u);
drawdblarrow (14u,20u)--(14u,10u);
label.lft(btex \(d\) etex,(14u,16u));
picture Slant;
Slant=currentpicture; %запоминаем
clearit; %очищаем текущую картинку
%рисуем воду когда пробирка стоит
fill (5u,0u)--(20u,0u)--(20u,10u)--(17u,10u)--
 (17u,3u)--(5u,3u)--cycle withcolor 0.7white;
%отрисовываем пробирку
draw Base;
%отрисовываем пробирку и наклоняем её
draw Slant yscaled 2/3 slanted 1/2 shifted (40u,0u);
endfig ;

В примере применяется возможность сохранить текущее состояние с помощью currentpicture, а так же возможность полностью очистить текущую картинку с помощью инструкции clearit.


Img 78 105 2.jpg

Наклон вертикально стоящей пробирки происходит с помощью масштабирования yscaled и, собственно, наклона slanted.

MetaPost поддерживает следующие базовые линейные преобразования:

Команда Результат
(x,y) shifted (a,b) (x+a,y+a)
(x,y) scaled s (sx,sy)
(x,y) xscaled s (sx,y)
(x,y) yscaled s (x,sy)
(x,y) slanted s (x+sy,y)
(x,y) rotated (x cos - y sin , x sin + y cos )
(x,y) zscaled (a,b) (xa-yb, xb+ya)

Кроме перечисленных базовых преобразований полезными для использования являются макросы rotatedaround ((a,b), c) — поворот вокруг точки (a,b) на угол c и reflectedabout (z1,z2) — отражение относительно линии, проходящей через точки z1 и z2.

MetaPost поддерживает объекты типа transform, то есть можно определить любое необходимое для вас преобразование, чтобы использовать его в дальнейшем. 

transform t;
t:= identity yscaled 2/3 slanted 1/2 shifted (40u,0u)
draw Slant transformed t;

Используемая при описании преобразования t константа identity тоже является преобразованием. identity – это «пустое» преобразование, то есть преобразование, которое ничего не делает (математически, оператор такого преобразования описывается единичной матрицей – identity matrix, что и определяет название).

Циклы и условные операторы

Циклы и условные операторы в MetaPost отличаются от того, что обычно есть в других языках программирования. Цикл не просто повторяет перечисленные в теле цикла инструкции — он дублирует текст, то есть внутри цикла не обязательно должна находиться синтаксически законченная конструкция. Это же относится и к условным операторам.

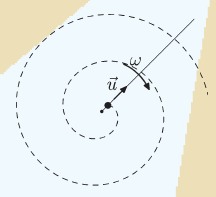
«Шарик с постоянной скоростью движется вдоль спицы, которая с вращается с постоянной угловой скоростью. Требуется изобразить траекторию шарика.»


Img 78 106 1.jpg

Для изображения траектории надо построить минимодель явления и задать физические параметры: поступательную скорость вдоль спицы v, угловую частоту w и начальные условия r и phi. Сама траектория создаётся с помощью следующего кода: 

%Файл cycle.mp
v:=27u;w:=360;N:=2.1;phi:=45;r:=5u;n:=100;
path p; pair O;
O:=(r*cosd(phi),r*sind(phi));
p:=O for i=0 upto n:
    ..((r+v*N*i/n)*dir(-w*N*i/n)+phi))
  endfor;
draw p withpen pencircle scaled 0.5u dashed evenly scaled 1u;

Декларация upto - это сокращение для step 1 until. Аналогично downto является сокращением для step -1 untull.

Формальный синтаксис цикла представлен ниже: 

for i=x1 step x_2 until x3: text(i) endfor

Это одна из форм, которая поддерживается META. Ещё одна форма представляет бесконечный цикл: 

forever: “текст” endfor

Для того чтобы выйти из подобного цикла необходимо воспользоваться конструкцией вида: 

exitif (“булево выражение”)

Булево выражение может быть переменной типа boolean (true/false) или результатом сравнения чисел, точек, путей или преобразований. Операторы сравнения почти совпадают с операторами сравнения языка C, за исключением оператора равенства «=» и оператора неравенства «<>». Выражение можно инвертировать с помощью приставки not и объединить с другим с помощью приставок and или or.

Формальный синтаксис условного оператора представлен ниже: 

if (“булево выражение1”): “текст1”
elseif (“булево выражение2”): “текст2”
else: “текст3” fi

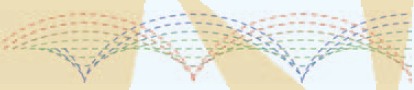
Воспользуемся циклами для изображения циклоиды — траектории точки на катящемся колесе.


Img 78 106 3.jpg

Обратите внимание, что в конце цикла или условного оператора нет необходимости ставить «;» это позволяет использовать их довольно изощрённым образом. 

%Файл cycle.mp 
%Рис к задаче 1.5.8 (20x120) - циклоида
beginfig(1) ;
numeric u;u = 0.8mm;
numeric R; R=10u;
path p,cycl;
p:=(-R,0u)..(R,0u)..cycle;
%колесо
draw p withpen pencircle scaled 0.3u
                   dashed withdots scaled 0.5u;
numeric j,n,v,w,phi,nsteps;
j=0;n=100;v=109.8u;w=-(v/R)*180/3.14;phi=180;nsteps=4;
numeric r,i;
for i:=0 upto 2*nsteps:
  r:=R-1/nsteps*R*i;
  %метки
  for j:=0 step n/4 until n:
    draw (j*(v/n)+r*cosd(j*(w/n)+phi),r*sind(j*(w/n)+phi))
      withpen pencircle scaled 1u;
  endfor;
  %траектория меток
  cycl:=for j:=0 upto n:
    if j<>0:..fi
         (j*(v/n)+r*cosd(j*(w/n)+phi),r*sind(j*(w/n)+phi))
  endfor;
  draw cycl dashed evenly scaled 1/2u
    withcolor (max(1-i/nsteps,0)*red+
              min(i/nsteps,2-i/nsteps)*green+
              max(i/nsteps-1,0)*blue);
 endfor;
endfig ;

В этом коде выражение if j<>0:..fi использовалось для того, чтобы перед первой точкой пути, описывающем циклоиду, не было декларации соединения. Я не знаю, какой еще из «популярных» на сегодня языков обладает такой способностью.

Макросы

Пользовательские функции в META фактически заменяются макросами. Как следствие, функции могут вернуть любую конструкцию: от числа до картинки.

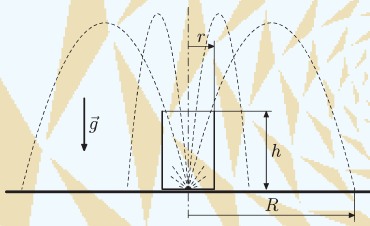
Одним из моих ранних рисунков на META был «взрыв» в стакане. Требовалось изобразить траекторию «осколков» которые летят по параболе и найти самую дальнюю точку, которую достигают осколки при таком «взрыве».


Img 78 106 2.jpg

Была написана процедура, которая рисовала параболу по переданным параметрам. Вызов выглядел примерно следующим образом: 

Parabola_dashed(0u,0u,-1.25angle(20/sqrt(8),
          10*sqrt(8)),10*sqrt(8)*u,0,100,1);

Сам макрос для отрисовки параболы представлен ниже. 

%Файл macros.mp
%Рисует параболу из точки (x,y) (полёт камня) штриховая
%линия. В качестве параметров передаётся (x,y), ang-угол,
%vel-скорость (100), %from,to - откуда и до куда рисовать
%параболу в процентах [0,100], mag - увеличение (0.8u)
%Для простоты g=10
def Parabola_dashed(expr x,y,ang,vel,from,to,mag) =
 path p;
 numeric t,g,n;
 picture dash_one;
 dash_one:=dashpattern(on 2mag off 2mag);
 n=100;%число шагов
 g=10.;
 t:=(2*vel*sind(ang)*from)/(g*n);
 p:=(vel*cosd(ang)*t*mag,(vel*sind(ang)*t-g*t*t/2)*mag);
 for i=from+1 upto to:
   t:=(2*vel*sind(ang)*i)/(g*n);
 p:=p..(vel*cosd(ang)*t*mag,
        (vel*sind(ang)*t-g*t*t/2)*mag);
endfor;
draw p shifted (x*mag,y*mag) dashed dash_one;
enddef;

Не самое удачное решение, но оно выполняло то, что от него требовалось. В подобных случаях лучше, чтобы в результате деятельности макроса оставался объект, который потом можно нарисовать с помощью команды draw и трансформировать по мере необходимости. Тогда функции передавалось бы гораздо меньше параметров, что значительно бы все упростило. Например, вызов для рисования пружинки, которая необходима в следующем примере, использует всего три входных параметра: 

draw Spring(25u,1.2u,25) rotated -90
 shifted (-12.5u,-20u) withpen pencircle scaled 0.1u;

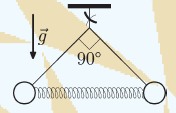
«Два тела, соединённые пружинкой, висят в поле тяжести на нитях, образующих угол в 900. В какой-то момент нить, крепящую конструкцию к потолку, разрывают.»


Img 78 107 2.jpg

Надо нарисовать пружинку. Изображение пружинка может пригодится много где ещё, поэтому оно было оформлено как макрос. 

%Файл macros.mp
%Создаёт пружину, высоты h, радиуса r, с числом витков n
% (0,0) - в основании пружины
vardef Spring(expr h,r,n) =
 begingroup save i;
   (0,0)--(0,-r/2+0.5h/n){dir 180}
   for i=h/n step h/n until h:
     ..tension 1.2..(-r,i-h/n)..tension 1.2 ..
     (0,r/2+i-0.5h/n)..tension 1.2 ..(r,i)..
     tension 1.2 ..(0,-r/2+i+0.3h/n){dir 180}
   endfor--(0,h)
 endgroup
enddef;

Обратите внимания на инструкцию tension — натяжение. Она говорит с какой «силой» надо «натянуть» соединение между точками. Значение 1.2 означает, что это следует сделать чуть потуже, чем обычно. С помощью этой инструкции описывается соединение между точками в определении пути типа «натянутая прямая»: 

def --- = ..tenstion infinity.. enddef;

Если отрисовка параболы является аналогом процедуры, то создание пружины аналогом функции. Вызовы begingroup endgroup позволяют обособить вычисления, проводящиеся между ними, от «внешнего мира». С помощью команды save можно защитить переменные внутри группы — «сохранённые» таким образом переменные восстанавливают свои значения после выхода за пределы endgroup.

Параметры, которые передаются внутрь макроса, перечисляются после декларации expr. Чтобы что-то вернуть в результате исполнения макроса, возвращаемое выражение надо поместить в конце макроса без завершающего символа «;».

Отличие vardef от def заключается в том, что в случае def в качестве названия макроса передаётся «символьная лексема», а в случае vardef «объявляемая переменная». Отличие между этими понятиями заключается в том, что объявляемая переменная может состоять из нескольких символьных лексем. Таким образом вы можете создавать переменные с модифицирующимися именами. Если вам этого не надо, то используйте def.

Средства поддержки макросов в MetaPost исключительно мощные и разнообразные. В частности, с помощью инструкции primarydef можно доопределить недостающие бинарные операторы.

Стандартные функции

Лучший способ облегчить себе жизнь при написании программы - это не писать её, а воспользоваться уже готовыми компонентами. META является специализированным языком, поэтому число стандартных функций не очень велико, но их выбор весьма показателен.

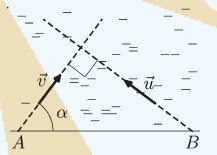
«Из точек A и B в море вышли два корабля...» Требуется изобразить поверхность воды:


Img 78 107 1.jpg

При кодировании этого рисунка использовалась функция генерации случайных чисел: 

uniformdeviate n

В результате выполнения функции получалось случайное число в интервале [0,1]. Кроме упомянутой функции в META есть ещё один генератор случайных чисел normaldeviate — он создает числа в соответствии с распределением Гаусса (~exp(–x/2)).

Хотелось бы упомянуть о возможности разлагать сложные объекты на составляющие, например: 

 numeric x[ ],y[ ];
 pair A,B; A=(x1,y1);A=(x2,y2);
 %A=(xpart x1,ypart y1)
 color c; c=(r,g,b);
 %c=(redpart c,greenpart c,bluepart c)
 path p;
 p=A--B;
 %A = point 0 of p = point 2 of p
 %B = point 1 of p = point length p of p

Таким образом можно «разобрать» на части любой путь, причём номер точки не обязательно должен быть целым (берётся точка на линии соединения в соответствии с дробной частью). С помощью функции length можно узнать число заданных точек в пути, а с помощью arclength — его длину.

К уже известным вычислительным функциям sqrt, abs, mod, round, sind и cosd полезно добавить mlog (f(x)=256 ln x) и mexp (f(x)=exp(x/256)).

Для операций с точками будут полезны функции angle (x,y) — вычисления угла наклона к оси абсцисс для вектора ((0,0)--(x,y)) в градуcах (операция, обратная dir a) и unitvector (x,y) — единичный вектор из начала координат.

Полный список стандартных функций представлен в «A User’s Manual for MetaPost» Джона Хобби. Этот текст идёт со стандартной поставкой LaTeX в виде файла mpman.pdf.

Источник — «http://wiki.linuxformat.ru/wiki/index.php?title=LXF78:MetaPost&oldid=4641»
Персональные инструменты
купить
подписаться
Яндекс.Метрика