Журнал LinuxFormat - перейти на главную

LXF106:SciLab

Материал из Linuxformat
Версия от 07:57, 24 августа 2009; Crazy Rebel (обсуждение | вклад)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)
Перейти к: навигация, поиск
Подписка на печатную версию
Весь 2015 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)
Подписка на электронную версию
Весь 2015 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)
Подшивки старых номеров журнала (печатные версии)
Весь 2014 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)

Содержание

SciLab: Основы

Компьютеры, как известно, придумывали для работы с числами, и для решения этой задачи были созданы самые различные программы. Александр Бикмеев покажет вам одну из них – свободный аналог Matlab.

В научной и инженерной среде хорошо известны так называемые CAS – Computer Algebra System; в русскоязычной литературе их часто называют СКМ – системами компьютерной математики. Одним из ярких представителей данного класса продуктов является Matlab, который с успехом применяется во многих областях науки и техники, более того, существует в виде Linux-версии. Но даже на Западе Matlab по карману не каждому вузу. И вот тут-то на сцене появляется супермен из мира свободного ПО – SciLab (http://www.scilab.org).

SciLab – это система компьютерной математики с открытым кодом. На момент написания статьи стабильной была версия 4.1.2. В установочный комплект включена подробнейшая справка, доступная на английском и французском языках: желающие могут загрузить ее с официального сайта в PDF-формате.

Задачей данной серии статей является обратить ваше внимание на данный продукт, показать некоторые его возможности и, если получится, избавить вас от Matlab-зависимости. Очень бы хотелось, чтобы статьи попали в руки тех преподавателей вузов, которые все еще ведут занятия на пиратском Matlab – быть может, SciLab станет для них более законным решением.

Подготовка к работе и запуск

Установить SciLab можно из RPM/Deb-пакета (http://rpmfind.net поможет в поиске первых), архива с исходными текстами или в виде бинарной сборки. Процедура во всех случаях будет стандартной. Для старта системы необходимо набрать в консоли команду scilab или, что значительно удобнее, создать на рабочем столе или в меню ссылку на приложение.


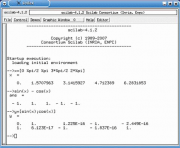
(thumbnail)
Главное окно SciLab с выполненными вычислениями.

После запуска вы увидите главное окно, в котором вводятся команды и выводятся результаты вычислений. В его верхней находится текстовое меню. Пункт меню Control содержит команды управления процессом вычислений: Resume [продолжить], Abort [отменить] и Stop [приостановить]. Пункт Help вызывает справку, а Editor открывает окно редактора файлов-сценариев. Пункт меню Graphic Windows # позволяет открывать и создавать графически окна, а также переключаться между ними. Самым интересным пунктом является Demos, выбор которого приводит к появлению окна со списком коллекции демонстрационных примеров. Погуляйте по ней – здесь есть очень много красивых проектов, особенно в разделе Simulation (рекомендую Demos > Simulation > Bike Simulation). Для знающих английский язык будет очень полезен первый пункт коллекции – Introduction to SCILAB, представляющий собой небольшой учебник.

Система SciLab является кросс-платформенной, но интерфейс ветки 4.х зависит от типа ОС. Так, в Windows он более приятный, имеет панель инструментов, а также поддерживает двунаправленную работу с буфером обмена. Linux-версия SciLab лишена этих возможностей. Как и при работе с графической консолью, вы можете вставить текст из буфера при помощи Shift+Ins, но скопировать что-то из окна SciLab не получится. Впрочем, скоро все изменится (см. Смена версий).

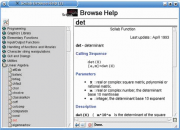
(thumbnail)
Окно справочной системы SciLab. Кнопка слева вверху переключает режимы структуры и поиска. Кнопки внизу окна текста справки позволяют перемещаться вперед и назад по уже открывавшимся темам.
(thumbnail)
Окно коллекции демонстрационных примеров SciLab. Обязательно посетите – здесь много интересного.

Продукт поставляется с большим руководством, описывающим все имеющиеся функции. Для того, чтобы вызвать окно справки, необходимо выбрать пункт меню Help > Help browser либо выполнить команду help. При этом, если вы ничего не меняли, откроется внутренний обозреватель справки. Однако, поскольку документация представляет собой набор html-файлов, вы можете изменить настройки и читать ее в любом удобном вам web-браузере. Для выбора приложения просмотра справки следует воспользоваться пунктами меню Help > Configure. Обычно вам предлагаются Firefox, Nautilus, Netscape, Opera и два варианта SciLab Browser – старый (old) и обычный. Наиболее удобен, на мой взгляд, обычный SciLab Browser, потому что только он предоставляет возможность поиска по всем файлам справки.

Вы можете также искать по части слова в описании или названии функции. Для этого следует выбрать пункт Help > Apropos, ввести в появившемся диалоге искомую подстроку и нажать кнопку OK. Откроется окно выбранного вами обозревателя справки с перечнем пунктов, удовлетворяющих условию поиска. Например, если вам необходимо узнать, как считаются интегралы, то для поиска можно ввести слово integral. После нажатия кнопки OK, мы увидим около десяти пунктов справки, содержащих данное слово.

Стандартное справочное описание содержит четыре раздела:

  • Calling Sequence [описание вызова] – шаблон вызова данной функции или процедуры
  • Parameters [Параметры] – описание всех возможных параметров текущей функции или процедуры
  • Description [Описание] – описание смысла самой функции или процедуры с примером использования.
  • See Also [Смотри также] – перечень схожих функций или процедур. Каждый предлагаемый вариант представляет собой гиперссылку, позволяющую перейти к его описанию.

Дополнительные пакеты расширений могут иметь свои собственные разделы, так что их полное перечисление здесь не имеет смысла. И пусть справка практически абсолютно не пригодна для изучения пакета – это именно справка – но постоянно обращение к ней поможет быстрее освоить систему.

Простые вычисления

Теперь, я надеюсь, вы сможете ориентироваться в небогатом интерфейсе SciLab, и мы можем перейти непосредственно к работе.

Итак, SciLab – это, преимущественно, система численных вычислений. Средства аналитического счета есть, но, во-первых, их немного, а, во-вторых, их использование неочевидно.

Как и в Matlab, команды набираются пользователем и выполняются системой последовательно. Ввод происходит в строке после системного приглашения, которое имеет вид -->. После набора команды ее уже нельзя исправить, как в текстовом редакторе: необходимо вернуться к ней при помощи клавиш-стрелок (как в терминале), потом внести изменения и нажать Enter, то есть вновь выполнить уже исправленную команду. Благодаря сходству с консолью, строку с приглашением называют «командной строкой SciLab».

После каждой команды в рабочем окне появляется результат. Если это не требуется (например, вы просто определяете значение переменной или функцию), то в конце команды следует поставить символ ; (точка с запятой). Если переменная-приемник не указана, то результат заносится в ans.

Длинные команды можно разбить на несколько строк, добавляя в конце каждой из них две или более точек подряд (..). Возможен также ввод поясняющего текста (комментария). Любой комментарий в SciLab, как и в языке C/C++, начинается с двойного символа //. Однако, следует отметить, что версия 4.1.2 не поддерживает кириллицу.

Самым простым случаем является использование SciLab в качестве калькулятора. Вы вводите какое-то математическое выражение с конкретными числами, нажимаете Enter и получаете результат. Например: 

--> 2.3*14 – sin(2.1) + tanh(0.2)
ans =
31.534166

Математические выражения строятся при помощи стандартных арифметических операций: «+» – сложение, «-» – вычитание, «*» – умножить, «/» – разделить, «^» – возведение в степень. Кроме того, вы можете использовать элементарные математические функции, только следует помнить, что SciLab разрабатывался за рубежом и использует западную нотацию, то есть, tan вместо tg, log вместо ln и так далее.

По умолчанию результат имеет семь цифр после запятой, но вы можете изменить это при помощи функции форматирования printf, синтаксис которой полностью схож с языком С. Например, для того, чтобы вывести результат предыдущего выражения с 10 знаками после запятой, введите: 

--> printf("%1.10f",2.3*14 – sin(2.1) + tanh(0.2))
ans =
31.5341659536

Конечно, использование такой мощной системы в качестве простого калькулятора бессмысленно. А при организации сложных вычислений мы неизбежно приходим к переменным, то есть специальным именованным ячейками памяти для хранения исходных и промежуточных данных, а также результата. Например, пусть нам необходимо найти длину и площадь окружности, а также объем и площадь поверхности шара по известному радиусу. В этом случае мы можем ввести переменную R для хранения значения радиуса: 

-->R=2; // Значение радиуса
-->l = 2*%pi*R
l =
12.566371
-->s = %pi*R^2
s =
12.566371
-->S3D = 4*%pi*R^2
S3D =
50.265482
-->V = 4/3*%pi*R^3
V =
33.510322

Вы могли заметить, что в качестве числа π используется конструкция, начинающаяся с символа процента. Так записываются системные переменные. Рассмотрим наиболее важные из них:

 %i – мнимая единица ( q1);
 %e – число e=2.7182818;
 %inf – машинный символ бесконечности (∞);
 %NaN – неопределенный результат (0/0, ∞/∞, 1∞ и т. п.);
 %eps – условный ноль %eps=2.220Е-16.

Переменные пользователя сохраняют свое значение до конца сеанса, либо до тех пор, пока не будут уничтожены командой clear. Просмотреть список всех активных переменных можно при помощи команды who. Команда whos() выводит более подробный перечень с указанием типа переменных (детали см. в справке).

Во время работы часто бывает необходимо сохранить выполненные действия и результаты в файл для дальнейшего использования. Это особенно актуально в связи с тем, что, как мы знаем, SciLab 4.x не поддерживает буфер обмена и прокрутку. Для записи рабочей сессии существует команда diary. Она принимает путь к файлу, например, diary('/home/username/session1.txt'). В конце, следует подать команду diary(0), которая останавливает запись. Тогда все команды и результаты будут сохранены в /home/username/session1.txt в обычном текстовом формате.

Кроме того, SciLab ведет историю введенных команд (но не результатов). Ее тоже можно записать в файл командой savehistory('путь и имя файла'). Записанная история загружается командой loadhistory('путь и имя файла'), стереть ее можно командой resethistory, ну а вывести на экран – командой gethistory. Запись истории команд в файл полезна в том случае, когда вы пытаетесь создать свою собственную функцию или файл-демонстрацию, но об этом поговорим в другой раз.


Векторы и матрицы

В Linux существует много продвинутых научных калькуляторов. Так чем же SciLab лучше? А тем, что он прекрасно работает с матрицами, векторами и вообще массивами чисел. Для того, чтобы создать строку (математически – вектор-строку) чисел, вам достаточно ввести их, разделяя пробелом или запятой и заключив в квадратные скобки, а чтобы ввести столбец (вектор-столбец), необходимо разделять числа символом точка с запятой (;): 

-->Vec_x=[1 2 3 4]
Vec_x =
1. 2. 3. 4.
-->Vec_y=[1;2;3;4]
Vec_y =
1.
2.
3.
4.

Ввод матрицы происходит по строкам (они разделяются точкой с запятой), между элементами строк ставятся запятые или пробелы. 

-->matr=[1 2 3; 4 5 6; 7 8 9]
matr =
1. 2. 3.
4. 5. 6.
7. 8. 9.

К любому элементу вектора или матрицы можно обратиться посредством индекса, заключенного в круглые скобки; если это элемент матрицы, то индексы разделяются запятой. Например, изменим главную диагональ введенной матрицы: 

-->matr(1,1) = 0;matr(2,2)=0;matr(3,3)=0;
-->matr
matr =
0. 2. 3.
4. 0. 6.
7. 8. 0.

Вы можете обратиться не только к элементу, но и к строке или столбцу, при этом вы должны указать его номер, а на месте второго индекса поставить : (двоеточие). Давайте поменяем местами первую строку с третьим столбцом. При этом нам придется столкнуться еще с одной операцией – транспонированием. Для ее выполнения необходимо ввести символ одинарной кавычки рядом с переменной-матрицей: 

-->tr=matr(1,:); tc=matr(:,3); // выделяем 1-ю строку и 3-й столбец
-->matr(1,:)=tc'; matr(:,3)=tr'; // транспонируем и записываем в
// 1-ю строку элементы 3-го столбца
// в 3-й столбец элементы 1-ой строки
-->matr
matr =
3. 6. 0.
4. 0. 2.
7. 8. 3.

Следует помнить и еще об одном правиле: при работе с векторами и матрицами действуют матричные правила выполнения арифметических действий. Например, умножение векторов Vec_x и Vec_y дает разные результаты в зависимости от порядка множителей: 

-->Vec_x*Vec_y
ans =
30.
-->Vec_y*Vec_x
ans =
1. 2. 3. 4.
2. 4. 6. 8.
3. 6. 9. 12.
4. 8. 12. 16.

как и должно быть по правилам матричной алгебры. Для того, чтобы выполнить поэлементное арифметическое действие (то есть перемножение не самих векторов, а только их соответствующих элементов: первый на первый, второй на второй и т. д.) используется символ операции с точкой в начале, при этом перемножаемые векторы должны иметь одинаковую размерность: 

-->Vec_x .* Vec_y
!--error 9999
inconsistent element-wise operation
-->Vec_x .* Vec_y'
ans =
1. 4. 9. 16.

В первом случае мы пытались выполнить поэлементное умножение строки на столбец и потому была выдана ошибка: размерность Vec_x – 1x4, а Vec_y – 4х1. Во втором случае мы транспонировали столбец и оба множителя стали одинаковой размерности – 1х4.

Выполним одно из простых действий – решим систему линейных уравнений методом обратной матрицы. Пусть дана система:

<math> \left\{\begin{array}{lcc} x-2y+z=2 \\ 2x+y-3z=-1 \\ x+3y+z=1 \\ \end{array}\right. </math>

тогда для ее решения нам потребуется подать следующие команды (для сокращения выводится только результат): 

-->A=[1 -2 1; 2 1 -3; 1 3 1];
-->b = [2; -1; 1];
-->x = inv(A)*b
x =
0.8
- 0.2
0.8

Построение графиков

Вектора и матрицы можно не только вводить вручную, но и формировать автоматически, используя конструкцию <начальное значение>:<шаг>:<конечное значение>. Например, сформируем вектор из чисел от 1 до 3 с шагом 0.2: 

-->vec=1:0.2:3
vec =
1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3.

Если шаг не указывается, то он принимается равным единице, скажем: 

-->vec2=1:3
vec2 =
1. 2. 3.

Сформированный вектор может использоваться как обычная переменная, то есть участвовать в математических операциях и быть аргументом функций. В последнем случае получится вектор, каждый элемент которого есть результат действия функции на элемент исходного вектора. 

-->Y=sin(vec2)
Y =
0.8414710 0.9092974 0.1411200

Таким образом можно довольно просто создавать таблицы функций, а от них два шага и до графика: достаточно просто сгенерировать вектор значений переменной и подать команду plot2d с указанием функции или перечня функций, заключенных в квадратные скобки и разделенных пробелом. При построении важно помнить, что на вход команды plot2d необходимо подавать вектор-столбцы значений функций, поэтому автоматически созданный вектор обычно необходимо транспонировать. 

-->x=[0:0.1:2*%pi]'; //создаем вектор и транспонируем его
-->plot2d(x, [sin(x) cos(x) sin(x).*cos(x)]) //строим графики

Если не указывать первый параметр (переменная х), то на графике по оси х будут отображаться просто порядковые номера значений в массиве. Обратите внимание, что для получения третьей функции мы использовали поэлементное умножение.

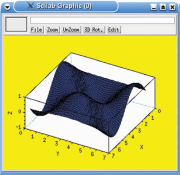
(thumbnail)
Результат выполнения команды plot3d.

Теперь давайте построим трехмерную поверхность. Для начала создадим два вектора с координатами x и y, затем – матрицу значений функции, причем здесь очень важен порядок множителей (вспомните комментарий выше): первым должен быть столбец (то есть любая из переменных), а вторым – строка (транспонированная переменная). После того, как мы получили все, что нужно, подаем команду plot3d: 

-->x=[0:0.1:2*%pi]';
-->y=x;
-->z=sin(4*x)*cos(y'/2);
-->plot3d(x,y,z)

Результат вы можете посмотреть на рисунке.

Хочется заметить, что многие из описываемых команд имеют дополнительные параметры, но мы не можем описать здесь их синтаксис полностью. Так что, если вам нужна дополнительная информация, то пройдитесь по приведенным во врезке ссылкам и, конечно же, покопайтесь во встроенной справке. До новых встреч!

Источник — «http://wiki.linuxformat.ru/wiki/index.php?title=LXF106:SciLab&oldid=8506»
Персональные инструменты
купить
подписаться
Яндекс.Метрика