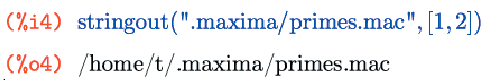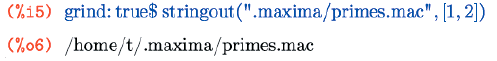Журнал LinuxFormat - перейти на главную

LXF86:Maxima

Материал из Linuxformat
(Различия между версиями)
Перейти к: навигация, поиск
(викификация, оформление)
 
(викификация, оформление)
Строка 64: Строка 64:
 
Здесь, чтобы было интереснее и не приходилось писать в файлы всякую ерунду, немного прервемся и создадим пару небольших
 
Здесь, чтобы было интереснее и не приходилось писать в файлы всякую ерунду, немного прервемся и создадим пару небольших
 
функций.
 
функций.
 +
 +
[[Изображение:LXF86_maxima02.png]]
 +
 +
Эта функция возвращает список всех простых чисел, меньших чем
 +
заданное целое число. Сначала мы проверяем, является ли аргумент
 +
целым числом и делаем это простейшим образом: в случае невыполнения условия оператор '''if''', напомню, вернет '''''false'''''. Генерируется список тоже самым простым и коротким в реализации способом – рекурсией.
 +
(примечание для людей, далеких от программирования: рекурсивная
 +
функция – это функция, вызывающая саму себя; чаще всего такие
 +
функции строятся по принципу индукции). Здесь используется функция ''Maxima'' по имени '''prev_prime()''', которая возвращает простое число, предшествующее заданному целому.
 +
 +
У рекурсии, при всей ее простоте реализации, есть неоспоримый
 +
минус – только один, но весьма существенный: чрезвычайная требовательность к объему памяти. Поэтому, для обеспечения возможности получать последовательности из больших простых чисел, добавим в наш учебный пример еще одну функцию:
 +
 +
[[Изображение:LXF86_maxima03.png]]
 +
 +
Смысл, думаю, понятен по аналогии с предыдущей: теперь мы еще
 +
и ограничили возвращаемый список снизу.
 +
 +
Теперь, когда у нас уже есть '''primesbetween()''', первую функцию можно написать по «принципу чайника» – сведя задачу к предыдущей:
 +
 +
[[Изображение:LXF86_maxima04.png]]
 +
 +
Теперь вернемся к '''stringout()'''. Эта функция, как и многие другие,
 +
может принимать несколько различных вариантов аргументов, первым из которых всегда выступает имя файла для записи, а остальные отвечают за то, что же именно будет туда записано. В варианте
 +
'''stringout(имя-файла, [начало, конец])''' записаны будут ячейки ввода с
 +
номерами от «начала» до «конца» включительно:
 +
 +
[[Изображение:LXF86_maxima05.png]]
 +
 +
$ cat .maxima/primes.mac
 +
primes(n):=if integerp(n) then (if n <= 2 then [] else append(primes(prev_
 +
prime(n)),[prev_prime(n)]));
 +
primesbetween(n,m):=if integerp(n) and integerp(m) then (if m <= 2 or
 +
prev_prime(m) <= n then [] else append(primesbetween(n,prev_
 +
prime(m)),[prev_prime(m)]));
 +
 +
Как видите, по умолчанию вывод получается не слишком красивым, поэтому сразу рассмотрим один ключ, влияющий на его формат.
 +
Долго рассказывать о нем смысла нет, лучше показать на примере:
 +
 +
[[Изображение:LXF86_maxima06.png]]
 +
 +
$ cat .maxima/primes.mac
 +
primes(x):=if integerp(x)
 +
      then (if x <= 2 then []
 +
              else append(primes(prev_prime(x)),[prev_prime(x)]));
 +
primesbetween(n,m):=if integerp(n) and integerp(m)
 +
            then (if m <= 2 or prev_prime(m) <= n then []
 +
                    else append(primesbetween(n,prev_prime(m)),
 +
                            [prev_prime(m)]));
 +
 +
Представления о правилах отступов у создателей этой опции
 +
несколько специфичные, но тем не менее, результат стал намного читабельнее. Так что, если вы планируете сохранять выражения
 +
''Maxima'' не только для того, чтобы потом загружать их обратно, а желаете редактировать созданные файлы, я рекомендую вам прописать '''grind:true''' глобально в файле '''~/.maxima/maxima-init.mac'''.
 +
 +
Идем дальше. С помощью ключевого слова '''input''' можно выгрузить в файл все ячейки ввода разом:
 +
 +
[[Изображение:LXF97_maxima07.png]]
 +
 +
$ cat primes-sample.mac
 +
primes(n):=if integerp(n)
 +
      then (if n <= 2 then []
 +
              else append(primes(prev_prime(n)),[prev_prime(n)]));
 +
primesbetween(n,m):=if integerp(n) and integerp(m)
 +
            then (if m <= 2 or prev_prime(m) <= n then []
 +
                    else append(primesbetween(n,prev_prime(m)),
 +
                            [prev_prime(m)]));
 +
primes1(n):=primesbetween(1,n);
 +
stringout(“.maxima/primes.mac”,[1,2]);
 +
grind:true;
 +
stringout(“.maxima/primes.mac”,[1,2]);
 +
(N:[random(100000)],for i thru 9 do N:append(N,[N[i]+random(100000)]),N);
 +
(P:[],for i thru 10 do P:append(P,primesbetween(N[i]-50,N[i])),P);
 +
 +
Кроме input, есть еще два ключевых слова: '''functions''' и '''values'''.
 +
Первое позволяет записать определения всех функций, второе – присвоение всем символам выражений их текущих значений:
 +
 +
[[Изображение:LXF97_maxima08.png]]
 +
 +
$ cat .maxima/primes.mac
 +
primes(n):=if integerp(n)
 +
      then (if n <= 2 then []
 +
              else append(primes(prev_prime(n)),[prev_prime(n)]));
 +
primesbetween(n,m):=if integerp(n) and integerp(m)
 +
            then (if m <= 2 or prev_prime(m) <= n then []
 +
                    else append(primesbetween(n,prev_prime(m)),
 +
                            [prev_prime(m)]));
 +
primes1(n):=primesbetween(1,n);
 +
$ cat primes-sample.mac
 +
primes(n):=if integerp(n)
 +
      then (if n <= 2 then []
 +
              else append(primes(prev_prime(n)),[prev_prime(n)]));
 +
primesbetween(n,m):=if integerp(n) and integerp(m)
 +
            then (if m <= 2 or prev_prime(m) <= n then []
 +
                    else append(primesbetween(n,prev_prime(m)),
 +
                            [prev_prime(m)]));
 +
primes1(n):=primesbetween(1,n);
 +
N:[49900,61971,153219,244360,290427,347723,396481,465378,522906,568462];
 +
P:[49853,49871,49877,49891,61927,61933,61949,61961,61967,153191,
 +
244313,244333,
 +
  244339,244351,244357,290383,290393,290399,290419,347707,34771
 +
7,396437,
 +
  396443,396449,396479,465331,465337,465373,522857,522871,52288
 +
1,522883,
 +
  522887,568433,568439,568441,568453];
 +
 +
И кроме всего этого, функцию '''stringout()''' можно вызвать с непосредственным перечислением в аргументах конкретных выражений.
 +
В этом случае, надо заметить, будут сохраняться не ячейки, содержащие заданные выражения, а именно сами выражения. То есть, если
 +
перечислить символ, для которого задано значение, то в файл будет
 +
записано только это значение. С именами функций, заданными непосредственно, дело обстоит не лучше: функцию таким образом задать,
 +
по сути, вообще нельзя: если просто написать ее имя, то вместо функции будет подставлен одноименный символ (или его значение, если
 +
оно задано). Но из обеих ситуаций есть выход. Для функций – штатный: функция '''fundef''', которая принимает имя любой пользовательской
 +
функции и возвращает ее определение в точности в таком же виде, в
 +
каком оно было введено (или могло бы быть введено) в «командной
 +
строке» ''Maxima'', с точностью до пробелов:
 +
 +
[[Изображение:LXF86_maxima09.png]]
 +
 +
$ cat .maxima/primesbetween.mac
 +
primesbetween(n,m):=if integerp(n) and integerp(m)
 +
            then (if m <= 2 or prev_prime(m) <= n then []
 +
                    else append(primesbetween(n,prev_prime(m)),
 +
                            [prev_prime(m)]));
 +
$ cat .maxima/primes1.mac
 +
primes(n):=if integerp(n)
 +
      then (if n <= 2 then []
 +
              else append(primes(prev_prime(n)),[prev_prime(n)]));
 +
primes1(n):=primesbetween(1,n);
 +
 +
А для символов можно использовать небольшую хитрость: блокировать вычисление переданного выражения, а в нем написать сначала
 +
сам символ, а потом через двоеточие – его же, предварив знаком принудительного вычисления (два апострофа):
 +
 +
[[Изображение:LXF86_maxima10.png]]
 +
 +
  t:~$ cat random-primes.mac
 +
  P:[49853,49871,49877,49891,61927,61933,61949,61961,61967,153191,
 +
  244313,244333,
 +
    244339,244351,244357,290383,290393,290399,290419,347707,34771
 +
  7,396437,
 +
    396443,396449,396479,465331,465337,465373,522857,522871,52288
 +
  1,522883,
 +
    522887,568433,568439,568441,568453];
 +
 +
В довершение темы работы с файлами стоит обратить внимание еще на один момент: при загрузке файлы в текущем каталоге не ищутся – и как раз для него надо задавать путь, причем полный, а не через '''./имя-файла''':
 +
 +
[[Изображение:LXF86_maxima11.png]]
 +
 +
==«Прослушайте объявление»==
 +
 +
Теперь поговорим о функциях, позволяющих налагать определенные
 +
условия на выражения, которыми оперирует ''Maxima''. Таких функций существует две, и достаточно разноплановых; но определенная
 +
связь между ними есть, так как все условия, заданные ими на данный
 +
момент, хранятся в общей «базе». Первая из этих функций называется
 +
'''declare''' (объявлять). С ее помощью можно объявлять весьма разнооб-разные факты о произвольных символах или выражениях; синтаксис ее весьма прост: '''declare(имя, факт)''' или '''declare(имя1, факт1, имя2, факт2, ...)'''; факты задаются с помощью ключевых слов. Сами факты
 +
я бы разделил на три группы: «технические» факты ''Maxima'', позволяющие использовать наделенный ими символ некоторым специальным образом при вводе выражений; факты о символах (атомарных
 +
выражениях); и факты о значениях функций. К первым относятся, к
 +
примеру, свойства '''evflag''' и '''evfun''', о которых шла речь в описании функции '''ev'''; некоторые штатные функции обладают ими по умолчанию, а с помощью функции '''declare''' мы можем присвоить эти свойства любым
 +
другим, в том числе и пользовательским, функциям. Вторая группа
 +
фактов несет информацию о неизвестных; например, мы можем указать, что некоторая неизвестная является константой, или что ее значение – целое. И третья группа – примерно то же самое, но о функциях;
 +
примеры: четная функция '''(f(–x)=f(x))''', аддитивная '''(f(x+y)=f(x)+f(y))''' или
 +
целочисленная. Для краткости просто перечислим наиболее интересные из возможных фактов, сгруппировав соответственно трем упомянутым группам.
 +
 +
==Технические факты==
 +
 +
===evfun===
 +
 +
Позволяет применять функцию или переменную как опцию, то есть
 +
'''«выражение, имя-функции»''' вместо '''«имя-функции(выражение)»''' или
 +
'''«выражение, имя-переменной»''' вместо '''«имя-переменной:true; выражение»'''. Подробнее см. в [[LXF82:Maxima|LXF82]].
 +
 +
===bindtest===
 +
 +
Запрещает использовать символ в выражениях до присвоения ему
 +
значения. При таком использовании ''Maxima'' выдаст ошибку. Пример
 +
см. в документации.
 +
 +
===feature===
 +
 +
Делает заданное имя именем свойства (факта), что дает возможность
 +
использовать его точно так же, как все перечисленные здесь имена.
 +
 +
==Факты о символах==
 +
 +
===constant===
 +
 +
Имя трактуется как константа.
 +
 +
===scalar===
 +
 +
Имя трактуется как скалярная величина. На это также влияет флаг
 +
'''assumescalar''': если он равен '''true''', то все неопределенные символы воспринимаются как скаляры. Тут есть небольшая коллизия: если верить документации, то по умолчанию '''assumescalar''' равен '''false''', реально же в
 +
''Maxima 5.10.0'' он равен '''true'''.
 +
 +
[[Изображение:LXF86_maxima12.png]]
 +
 +
===nonscalar===
 +
 +
Имя трактуется как не-скалярная величина, то есть матрица или вектор.
 +
 +
===integer, noninteger===
 +
 +
Целое и нецелое число.
 +
 +
===even, odd===
 +
 +
Четное и нечетное целое число.
 +
 +
[[Изображение:LXF86_maxima13.png]]
 +
 +
==Факты о функциях==
 +
 +
===rassociative===
 +
 +
Объявляет функцию как «ассоциативную» по правому аргументу.
 +
 +
===lassociative===
 +
 +
Аналогично – по левому аргументу.
 +
 +
[[Изображение:LXF86_maxima14.png]]
 +
 +
===nary===
 +
 +
Объявляет «n-арную» функцию. Это и два предыдущих названия не
 +
совсем точны: n-арной правильно называть функцию от n аргументов,
 +
а лево- и право- ассоциативной – функции именно с односторонней
 +
ассоциативностью, то есть, для «лево-» '''f(f(a,b),c)[[Изображение:LXF85_maxima16.png]]f(a,b,c)[[Изображение:LXF85_maxima16.png]]f(a,f(b,c))'''. А
 +
в ''Maxima'' все три факта объявляют на самом деле полно-ассоциативную функцию от произвольного числа аргументов, а различаются только тем, как будут расставлены скобки по умолчанию.
 +
 +
[[Изображение:LXF86_maxima15.png]]

Версия 09:28, 23 декабря 2008

Подписка на печатную версию
Весь 2015 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)
Подписка на электронную версию
Весь 2015 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)
Подшивки старых номеров журнала (печатные версии)
Весь 2014 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)


Учебник Maxima Максимум свободысимвольных вычислений

Содержание

Работа c файлами

ЧАСТЬ 6 Завершая этот длинный цикл статей, Тихон Тарнавский коснется вопросов работы с файлами, базой данных фактов и напишет собственную функцию символьного дифференцирования!

В прошлый раз мы остановились на возможностях программирования, предназначенных для написания собственных функций и модулей к Maxima – и теперь для их полноценного использования рассмотрим несколько инструментов работы с файлами, позволяющих сохранять и загружать эти функции и модули на диск и с диска. Далее речь пойдет о наложении определенных условий на неизвестные и значения функций. Напоследок познакомимся с функциями по работе... с функциями: это один из очень мощных инструментов, позаимствованных из функционального программирования; а также разберем несколько более крупных учебных примеров, использующих многое из изученного нами во всех статьях цикла.

Учимся читать и писать

Среди средств для операций с файлами функции с наиболее очевидными именами – save и load – имеют, вопреки привычной для Maxima логичности всех названий, различный контекст. Первая предназначена для выгрузки Maxima-выражений в виде исходных кодов на Lisp, так что если вы не знаток Lisp (да и реализации внутренних механизмов Maxima), то эта функция представляет лишь чисто академический интерес. Посему подробнее мы займемся другими функциями – для обработки так называемых пакетных (batch) файлов, хранящих выра жения уже в синтаксисе самой Maxima. А поскольку в виде таких файлов поставляется немалое количество функционала Maxima, то начнем с загрузки. И вот о второй из очевидно-именуемых функций здесь уже будет рассказано.

Функции чтения файлов с выражениями Maxima существует три: demo(имя-файла), batch(имя-файла) и batchload(имя-файла). Первая предназначена для загрузки так называемых демо-файлов, задуманных, как и явствует из названия, для демонстрационных примеров. Она загружает демо-файл и выполняет его в пошаговом режиме, ожидая нажатия Enter после выполнения каждой строки. В составе Maxima поставляется значительное количество демо-файлов; упоминания о них можно найти в документации, а сами файлы несложно обнаружить среди содержимого пакета maxima-share (либо, в случае отсутствия такового в вашем дистрибутиве, просто maxima) по их расширению – .dem.

Функция batch() загружает Maxima-файл с расширением .mac или .mc (от первоначального названия программы – Macsyma) и выполняет содержащиеся в нем выражения так, как если бы они вводились прямо в текущей сессии, то есть с отображением результата каждого выражения и назначением меток %iN, %oN. Функция batchload(), напротив, подгружает пакетный файл «молча»: все назначенные в нем функции и переменные становятся доступны, но результаты не видны, и весь хранимый ввод-вывод, включая значения символов % и _ и результаты, возвращаемые функцией %th(), остается тем же, что и до вызова.

Функции batch() и batchload() используют при поиске файлов для загрузки путь (точнее сказать, шаблон, потому как в нем содержатся не только имена каталогов, но и допустимые расширения файлов), который хранится в переменной file_search_maxima. По умолчанию эта переменная содержит все каталоги, в которые устанавливаются .mac-файлы из пакетов Maxima, а также ~/.maxima, предназначенный для пользовательских файлов. Для других функций загрузки существуют отдельные переменные: file_search_lisp и file_search_demo, смысл которых понятен из их названий.

Ну и под конец здесь нужно вспомнить о вышеназванной функции load. Она, фактически, является оберткой над двумя функциями: уже описанной выше batchload() и loadfile(), вторая, совершенно аналогично первой, загружает файл, но уже не с выражениями Maxima, а с исходным кодом Lisp, то есть является парной к функции save(). Функцию load() можно, в принципе, использовать вместо batchload(): путь file_search_maxima задан в ней раньше, чем file_search_lisp, так что в случае неоднозначности она будет загружать файлы Maxima; а кроме того, так короче.

Некоторый функционал Maxima содержится в неподгружаемых автоматически внешних файлах, которые, соответственно, нужно принудительно загрузить перед использованием:

LXF86 maxima01.png

Помимо ручной загрузки нужного файла, можно также настроить Maxima на автоматическую подгрузку в случае вызова заданной функции. Делается это так: setup_autoload(имя-файла,имена-функций); нужные функции здесь перечисляются через запятую прямо после имени файла. Удобнее, конечно, будет не вызывать функцию setup_autoload() вручную (так в ней и толку немного), а настроить Maxima на автоматический ее запуск при старте программы. Файл, который, при его наличии, вызывается при каждом запуске Maxima, называется maxima-init.mac и самое логичное для него местоположение – все тот же каталог ~/.maxima. Конечно, он может содержать не только вызовы функции setup_autoload(), а любые выражения Maxima, которые вы хотите выполнять при каждом ее запуске. Использование этой функции может сделать вашу работу с Maxima намного более удобной в том случае, если вы часто используете некоторые из внешних функций Maxima или функции, вами же и написанные.

Для полноценного чтения файлов всего сказанного уже вполне достаточно, теперь перейдем к записи в них. Тут нас в первую очередь интересует функция stringout(), которая позволяет выгружать в файл любые выражения и функции Maxima в точно таком виде, в каком их загружают функции demo(), batch() и batchload(). С ее помощью можно писать выражения, которые вы хотите иметь во внешнем модуле, находясь непосредственно в интерфейсе Maxima, с последующей записью в этот самый модуль. Для выгрузки функций в один из стандартных каталогов Maxima (самым логичным вариантом будет, пожалуй, упомянутый выше ~/.maxima) имя файла во всех вариантах вызова функции stringout() нужно задавать с полным путем; в случае задания имени без пути файл будет создан в текущем каталоге, то есть в том, откуда производился запуск Maxima.

Здесь, чтобы было интереснее и не приходилось писать в файлы всякую ерунду, немного прервемся и создадим пару небольших функций.

LXF86 maxima02.png

Эта функция возвращает список всех простых чисел, меньших чем заданное целое число. Сначала мы проверяем, является ли аргумент целым числом и делаем это простейшим образом: в случае невыполнения условия оператор if, напомню, вернет false. Генерируется список тоже самым простым и коротким в реализации способом – рекурсией. (примечание для людей, далеких от программирования: рекурсивная функция – это функция, вызывающая саму себя; чаще всего такие функции строятся по принципу индукции). Здесь используется функция Maxima по имени prev_prime(), которая возвращает простое число, предшествующее заданному целому.

У рекурсии, при всей ее простоте реализации, есть неоспоримый минус – только один, но весьма существенный: чрезвычайная требовательность к объему памяти. Поэтому, для обеспечения возможности получать последовательности из больших простых чисел, добавим в наш учебный пример еще одну функцию:

LXF86 maxima03.png

Смысл, думаю, понятен по аналогии с предыдущей: теперь мы еще и ограничили возвращаемый список снизу.

Теперь, когда у нас уже есть primesbetween(), первую функцию можно написать по «принципу чайника» – сведя задачу к предыдущей:

LXF86 maxima04.png

Теперь вернемся к stringout(). Эта функция, как и многие другие, может принимать несколько различных вариантов аргументов, первым из которых всегда выступает имя файла для записи, а остальные отвечают за то, что же именно будет туда записано. В варианте stringout(имя-файла, [начало, конец]) записаны будут ячейки ввода с номерами от «начала» до «конца» включительно:

LXF86 maxima05.png 

$ cat .maxima/primes.mac
primes(n):=if integerp(n) then (if n <= 2 then [] else append(primes(prev_
prime(n)),[prev_prime(n)]));
primesbetween(n,m):=if integerp(n) and integerp(m) then (if m <= 2 or
prev_prime(m) <= n then [] else append(primesbetween(n,prev_
prime(m)),[prev_prime(m)]));

Как видите, по умолчанию вывод получается не слишком красивым, поэтому сразу рассмотрим один ключ, влияющий на его формат. Долго рассказывать о нем смысла нет, лучше показать на примере:

LXF86 maxima06.png 

$ cat .maxima/primes.mac
primes(x):=if integerp(x)
      then (if x <= 2 then []
              else append(primes(prev_prime(x)),[prev_prime(x)]));
primesbetween(n,m):=if integerp(n) and integerp(m)
           then (if m <= 2 or prev_prime(m) <= n then []
                   else append(primesbetween(n,prev_prime(m)),
                           [prev_prime(m)]));

Представления о правилах отступов у создателей этой опции несколько специфичные, но тем не менее, результат стал намного читабельнее. Так что, если вы планируете сохранять выражения Maxima не только для того, чтобы потом загружать их обратно, а желаете редактировать созданные файлы, я рекомендую вам прописать grind:true глобально в файле ~/.maxima/maxima-init.mac.

Идем дальше. С помощью ключевого слова input можно выгрузить в файл все ячейки ввода разом:

Файл:LXF97 maxima07.png

$ cat primes-sample.mac 

primes(n):=if integerp(n)
      then (if n <= 2 then []
              else append(primes(prev_prime(n)),[prev_prime(n)]));
primesbetween(n,m):=if integerp(n) and integerp(m)
            then (if m <= 2 or prev_prime(m) <= n then []
                    else append(primesbetween(n,prev_prime(m)),
                            [prev_prime(m)]));
primes1(n):=primesbetween(1,n);
stringout(“.maxima/primes.mac”,[1,2]);
grind:true;
stringout(“.maxima/primes.mac”,[1,2]);
(N:[random(100000)],for i thru 9 do N:append(N,[N[i]+random(100000)]),N);
(P:[],for i thru 10 do P:append(P,primesbetween(N[i]-50,N[i])),P);

Кроме input, есть еще два ключевых слова: functions и values. Первое позволяет записать определения всех функций, второе – присвоение всем символам выражений их текущих значений:

Файл:LXF97 maxima08.png 

$ cat .maxima/primes.mac
primes(n):=if integerp(n)
      then (if n <= 2 then []
              else append(primes(prev_prime(n)),[prev_prime(n)]));
primesbetween(n,m):=if integerp(n) and integerp(m)
           then (if m <= 2 or prev_prime(m) <= n then []
                   else append(primesbetween(n,prev_prime(m)),
                           [prev_prime(m)]));
primes1(n):=primesbetween(1,n);
$ cat primes-sample.mac
primes(n):=if integerp(n)
      then (if n <= 2 then []
              else append(primes(prev_prime(n)),[prev_prime(n)]));
primesbetween(n,m):=if integerp(n) and integerp(m)
           then (if m <= 2 or prev_prime(m) <= n then []
                   else append(primesbetween(n,prev_prime(m)),
                           [prev_prime(m)]));
primes1(n):=primesbetween(1,n);
N:[49900,61971,153219,244360,290427,347723,396481,465378,522906,568462];
P:[49853,49871,49877,49891,61927,61933,61949,61961,61967,153191,
244313,244333,
  244339,244351,244357,290383,290393,290399,290419,347707,34771
7,396437,
  396443,396449,396479,465331,465337,465373,522857,522871,52288
1,522883,
  522887,568433,568439,568441,568453];

И кроме всего этого, функцию stringout() можно вызвать с непосредственным перечислением в аргументах конкретных выражений. В этом случае, надо заметить, будут сохраняться не ячейки, содержащие заданные выражения, а именно сами выражения. То есть, если перечислить символ, для которого задано значение, то в файл будет записано только это значение. С именами функций, заданными непосредственно, дело обстоит не лучше: функцию таким образом задать, по сути, вообще нельзя: если просто написать ее имя, то вместо функции будет подставлен одноименный символ (или его значение, если оно задано). Но из обеих ситуаций есть выход. Для функций – штатный: функция fundef, которая принимает имя любой пользовательской функции и возвращает ее определение в точности в таком же виде, в каком оно было введено (или могло бы быть введено) в «командной строке» Maxima, с точностью до пробелов:

LXF86 maxima09.png 

$ cat .maxima/primesbetween.mac
primesbetween(n,m):=if integerp(n) and integerp(m)
           then (if m <= 2 or prev_prime(m) <= n then []
                   else append(primesbetween(n,prev_prime(m)),
                           [prev_prime(m)]));
$ cat .maxima/primes1.mac
primes(n):=if integerp(n)
      then (if n <= 2 then []
              else append(primes(prev_prime(n)),[prev_prime(n)]));
primes1(n):=primesbetween(1,n);

А для символов можно использовать небольшую хитрость: блокировать вычисление переданного выражения, а в нем написать сначала сам символ, а потом через двоеточие – его же, предварив знаком принудительного вычисления (два апострофа):

LXF86 maxima10.png 

 t:~$ cat random-primes.mac
 P:[49853,49871,49877,49891,61927,61933,61949,61961,61967,153191,
 244313,244333,
   244339,244351,244357,290383,290393,290399,290419,347707,34771
 7,396437,
   396443,396449,396479,465331,465337,465373,522857,522871,52288
 1,522883,
   522887,568433,568439,568441,568453];

В довершение темы работы с файлами стоит обратить внимание еще на один момент: при загрузке файлы в текущем каталоге не ищутся – и как раз для него надо задавать путь, причем полный, а не через ./имя-файла:

LXF86 maxima11.png

«Прослушайте объявление»

Теперь поговорим о функциях, позволяющих налагать определенные условия на выражения, которыми оперирует Maxima. Таких функций существует две, и достаточно разноплановых; но определенная связь между ними есть, так как все условия, заданные ими на данный момент, хранятся в общей «базе». Первая из этих функций называется declare (объявлять). С ее помощью можно объявлять весьма разнооб-разные факты о произвольных символах или выражениях; синтаксис ее весьма прост: declare(имя, факт) или declare(имя1, факт1, имя2, факт2, ...); факты задаются с помощью ключевых слов. Сами факты я бы разделил на три группы: «технические» факты Maxima, позволяющие использовать наделенный ими символ некоторым специальным образом при вводе выражений; факты о символах (атомарных выражениях); и факты о значениях функций. К первым относятся, к примеру, свойства evflag и evfun, о которых шла речь в описании функции ev; некоторые штатные функции обладают ими по умолчанию, а с помощью функции declare мы можем присвоить эти свойства любым другим, в том числе и пользовательским, функциям. Вторая группа фактов несет информацию о неизвестных; например, мы можем указать, что некоторая неизвестная является константой, или что ее значение – целое. И третья группа – примерно то же самое, но о функциях; примеры: четная функция (f(–x)=f(x)), аддитивная (f(x+y)=f(x)+f(y)) или целочисленная. Для краткости просто перечислим наиболее интересные из возможных фактов, сгруппировав соответственно трем упомянутым группам.

Технические факты

evfun

Позволяет применять функцию или переменную как опцию, то есть «выражение, имя-функции» вместо «имя-функции(выражение)» или «выражение, имя-переменной» вместо «имя-переменной:true; выражение». Подробнее см. в LXF82.

bindtest

Запрещает использовать символ в выражениях до присвоения ему значения. При таком использовании Maxima выдаст ошибку. Пример см. в документации.

feature

Делает заданное имя именем свойства (факта), что дает возможность использовать его точно так же, как все перечисленные здесь имена.

Факты о символах

constant

Имя трактуется как константа.

scalar

Имя трактуется как скалярная величина. На это также влияет флаг assumescalar: если он равен true, то все неопределенные символы воспринимаются как скаляры. Тут есть небольшая коллизия: если верить документации, то по умолчанию assumescalar равен false, реально же в Maxima 5.10.0 он равен true.

LXF86 maxima12.png

nonscalar

Имя трактуется как не-скалярная величина, то есть матрица или вектор.

integer, noninteger

Целое и нецелое число.

even, odd

Четное и нечетное целое число.

LXF86 maxima13.png

Факты о функциях

rassociative

Объявляет функцию как «ассоциативную» по правому аргументу.

lassociative

Аналогично – по левому аргументу.

LXF86 maxima14.png

nary

Объявляет «n-арную» функцию. Это и два предыдущих названия не совсем точны: n-арной правильно называть функцию от n аргументов, а лево- и право- ассоциативной – функции именно с односторонней ассоциативностью, то есть, для «лево-» f(f(a,b),c)LXF85 maxima16.pngf(a,b,c)LXF85 maxima16.pngf(a,f(b,c)). А в Maxima все три факта объявляют на самом деле полно-ассоциативную функцию от произвольного числа аргументов, а различаются только тем, как будут расставлены скобки по умолчанию.

LXF86 maxima15.png

Источник — «http://wiki.linuxformat.ru/wiki/index.php?title=LXF86:Maxima&oldid=6159»
Персональные инструменты
купить
подписаться
Яндекс.Метрика