LXF80:MetaPost
Lockal (обсуждение | вклад) м (восстановление кавычек в коде AWB) |
Lockal (обсуждение | вклад) м ({{Цикл/MetaPost}}) |
||
| Строка 1: | Строка 1: | ||
| − | + | {{Цикл/MetaPost}} | |
| − | + | ||
| − | + | ||
| − | + | ||
== MetaPost Дополнительные главы == | == MetaPost Дополнительные главы == | ||
'''ЧАСТЬ 4 ''' | '''ЧАСТЬ 4 ''' | ||
Версия 22:14, 16 мая 2008
|
|
|
- Метамодернизм в позднем творчестве В.Г. Сорокина
- ЛитРПГ - последняя отрыжка постмодерна
- "Ричард III и семиотика"
- 3D-визуализация обложки Ridero создаем обложку книги при работе над самиздатом.
- Архитектура метамодерна - говоря о современном искусстве, невозможно не поговорить об архитектуре. В данной статье будет отмечено несколько интересных принципов, характерных для построек "новой волны", столь притягательных и скандальных.
- Литература
- Метамодерн
- Рокер-Прометей против изначального зла в «Песне про советскую милицию» Вени Дркина, Автор: Нина Ищенко, к.ф.н, член Союза Писателей ЛНР - перепубликация из журнала "Топос".
- Как избавиться от комаров? Лучшие типы ловушек.
- Что делать если роблокс вылетает на windows
- Что делать, если ребенок смотрит порно?
- Почему собака прыгает на людей при встрече?
- Какое масло лить в Задний дифференциал (мост) Visco diff 38434AA050
- О чем может рассказать хвост вашей кошки?
- Верветки
- Отчетность бюджетных учреждений при закупках по Закону № 223-ФЗ
- Срок исковой давности как правильно рассчитать
- Дмитрий Патрушев минсельхоз будет ли преемником Путина
- Кто такой Владислав Поздняков? Что такое "Мужское Государство" и почему его признали экстремистским в России?
- Как правильно выбрать машинное масло в Димитровграде?
- Как стать богатым и знаменитым в России?
- Почему фильм "Пипец" (Kick-Ass) стал популярен по всему миру?
- Как стать мудрецом?
- Как правильно установить FreeBSD
- Как стать таким как Путин?
- Где лучше жить - в Димитровграде или в Ульяновске?
- Почему город Димитровград так называется?
- Что такое метамодерн?
- ВАЖНО! Временное ограничение движения автотранспортных средств в Димитровграде
- Тарифы на электроэнергию для майнеров предложено повысить
Содержание[убрать] |
MetaPost Дополнительные главы
ЧАСТЬ 4
Всё описать невозможно, но никто не запрещает попробовать. Евгений Балдин представляет вашему вниманию заключительную серию учебника MetaPost.
Возможности META в то или иной мере уже изложены. В этой статье будут разобраны полезные приёмы, которые можно применять при кодировании картинок и описаны некоторые из стандартных пакетов, поставляемых с MetaPost.
Исходники стандартных MetaPost-пакетов обычно находятся в директории $(TEXMF)/texmf-dist/metapost/, а документация к ним – в директории $(TEXMF)/texmf-dist/doc/metapost/, где $(TEXMF) – корневая директория для дистрибутива LaTeX. Сказанное верно для TeX Live.
Пакет boxes
boxes – один из самых первых пакетов общего назначения, появившихся в MetaPost. Его предназначение – рисовать простые диаграммы. Он проектировался как более изощрённая замена для пакета Брайана Кернигана pic (man pic).
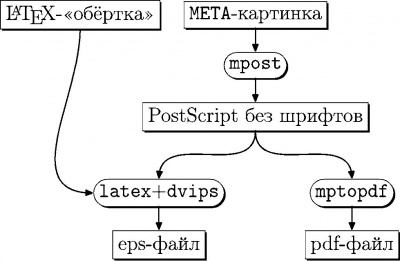
С другой стороны, функциональности этого пакета достаточно для автоматической генерации достаточно сложных зависимостей. В качестве примера разберём, как была реализована диаграмма, объясняющая действие MetaPost-конвейера во введении в цикл статей по MetaPost. (см. LXF76)
%Файл dop.mp
%в отличии от boxes здесь ещё определено окружение rboxit
input rboxes;
%определяем ещё один вид box'а
%параметры можно передавать и так
%expr - изолированные выражения
%text - абсолютно всё, что передаётся
vardef drawshadowed(expr dx,dy)(text t) =
fixsize(t);
forsuffixes s=t:
fill bpath.s shifted (dx,dy);
unfill bpath.s;
drawboxed(s);
% можно было напечатать только текст
% и не рисовать рамку
% draw pic(s) withcolor red;
endfor;
enddef;
%пример boxes
beginfig(2) ;
numeric u;u:=1mm;
%определяем box'ы
%определяем box с прямыми углами
boxit.a(btex \texttt{META}-картинка etex);
%определяем box с закруглёнными углами
rboxit.b(btex \texttt{metapost} etex);
%определяем жёсткую связь между a и b
b.n = a.s - (0,5u);
boxit.c(btex PostScript без шрифтов etex);
c.n = b.s - (0,5u);
rboxit.e(btex \texttt{latex}\(+\)\texttt{dvips} etex);
e.n=c.s-(20u,10u);
boxit.d(btex \LaTeX-<<обёртка>> etex);
d.e=a.w-(5u,0);
boxit.g(btex eps-файл etex);
g.n=e.s-(0,5u);
rboxit.h(btex \texttt{mptopdf} etex);
h.n=c.s-(-20u,10u);
boxit.i(btex pdf-файл etex);
i.n=h.s-(0,5u)
%разрешаем зависимости и рисуем boxes
drawshadowed(1/3u,-1/3u,a,b,c,d,e,g,h,i);
pickup pencircle scaled 0.3u;
%рисуем стрелки (сдвижка вида (0u,-1/3u) появилась,
%так как было определено новое окружение drawshadowed)
drawarrow a.s -- b.n-(0u,-1/3u);
drawarrow b.s -- c.n-(0u,-1/3u);
drawarrow c.s{dir -90} .. {dir -90}e.n-(0u,-1/3u);
drawarrow c.s{dir -90} .. {dir -90}h.n-(0u,-1/3u);
drawarrow e.s -- g.n-(0u,-1/3u);
drawarrow h.s -- i.n-(0u,-1/3u);
drawarrow d.s{dir -90} .. {dir 0}e.w-(1/3u,0u);
endfig;
Обратите внимание на ещё один вид цикла – forsuffixes. Эта запись позволяет разбирать произвольное число передаваемых аргументов.
Алгоритм создания диаграммы следующий:
• С помощью команд boxit, rboxit или circleit объявляем box. Имя box'a добавляется к команде через точку как суффикс. В данном примере определено 8 box'ов от «a» до «i» включительно.
• Составляем уравнения связей. Через точку к именам box'ов можно добавить один из восьми суффиксов: n – север (верхняя точка), s – юг (нижняя точка), w – запад (крайняя точка рамки слева), e – восток (крайняя точка рамки справа) и sw, bw, se, sw – комбинации уже перечисленных суффиксов, которые соответствуют углам рамки
Уравнение связи
b.n = a.s — (0,5u);
можно описать следующим образом: северная (верхняя) точка box'a «b» находится ниже южной (нижней) точки box'а «a» на 5u. При составлении уравнения связей следует пользоваться только знаком равенства. Это не присваивание, а именно уравнение, которое требуется разрешить.
• С помощью команды drawboxed нарисовать «закодированную» диаграмму. При исполнении этой команды разрешается система уравнений. По умолчанию, если не указать специально, box располагается в точке (0,0).
• Нарисовать стрелки между элементами диаграммы. Можно пользоваться именами box'ов со стандартными суффиксами.
Прежде чем использовать этот пакет, необходимо прочитать соответствующий раздел в руководстве пользователя по MetaPost Джона Хобби mpman.pdf.
Фейнмановские диаграммы
Простота MetaPost позволяет использовать его как базу для построений более высокого порядка. Существует несколько подобных LaTeX-пакетов. mfpic уже упоминался. В этом разделе описывается ещё один старейший пакет, созданный по данной технологии.
В 1995 году Торстен Охл (Torsten Ohl) представил пакет feynmp для рисования фейнмановских диаграмм. Фейнмановские диаграммы используются для вычисления сумм большого числа вкладов от элементарных процессов. В своё время эта технология довольно сильно продвинула технику вычислений в физике высоких энергий. Её можно использовать везде, где сложный процесс описывается с помощью элементарных приближений. Пакет feynmp – это пакет LaTeX, который для рисования диаграмм использует MetaPost.
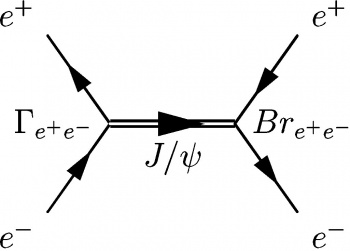
Интересующий меня с целью извлечения электронной ширины J/ резонанса процесс имеет в Борновском приближении следующий вид: Это несложная диаграмма, и если не считать метки, то для её описания требуется всего пять операторов:
%Файл eepsiee.tex
%пакет для рисования фейнмановских диаграмм
\usepackage{feynmp}
...
\begin{fmffile}{ee-psi-ee} %имя mp-файл
\begin{fmfgraph*}(110,62) %размер диаграммы
\fmfleft{ei,pi} %вершины-источники
\fmfright{eo,po} %исходящие вершины
\fmflabel{$e^-$}{ei} %метка источника e^-
\fmflabel{$e^+$}{pi} %метка источника e^+
\fmflabel{$e^+$}{po} %метка исходящей вершины
\fmflabel{$e^-$}{eo} %метка исходящей вершины
%линия соединяющая источники
\fmf{fermion}{ei,Ji,pi}
%линия соединяющие исходящее вершины
\fmf{fermion}{po,Jo,eo}
%Метка для начальной вершины промежуточной частицы
\fmflabel{$\Gamma_{e^{+}e^{-}}$}{Ji}
%Метка для конечной вершины промежуточной частицы
\fmflabel{$Br_{e^{+}e^{-}}$}{Jo}
%Соединительная линия
\fmf{heavy,label=$J/\psi$}{Ji,Jo}
\end{fmfgraph*}
\end{fmffile}
Окружение \begin{fmffile} в качестве параметра требует имя mp-файла, в который будут писать команды META. В данном примере имя файла определено как ee-psi-ee.mp. Для того, чтобы получить диаграмму, описанную в файле eepsiee.tex, были проделаны следующие действия:
> latex eepsiee.tex > mpost ee-psi-ee.mp > latex eepsiee.tex
После выполнения этих команд результат можно посмотреть с помощью программы xdvi или преобразовать dvi-файл в PostScript или pdf.
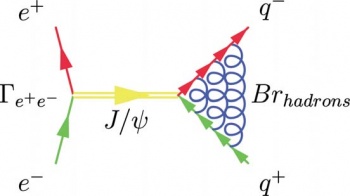
Следующая простейшая диаграмма не имеет особого смысла. Она просто демонстрирует возможности пакета:
«Сотрудничество» c MetaPost даёт возможность feynmp получить доступ к цвету. Цвет можно определять точно так же, как он определяется в MetaPost.
%Файл eepsihadr.tex
\begin{fmffile}{ee-psi-hadr}
\begin{fmfgraph*}(110,62)
\fmfleft{i1,i2}
\fmfright{o1,o2}
\fmflabel{$e^-$}{i1}
\fmflabel{$e^+$}{i2}
\fmflabel{$q^+$}{o1}
\fmflabel{$q^-$}{o2}
\fmf{fermion,foreground=green}{i1,v1}
\fmf{fermion,foreground=red}{v1,i2}
\fmf{fermion,foreground=green}{o1,v2,v3,v4,v5}
\fmf{fermion,foreground=red}{v5,v6,v7,v8,o2}
%изменяем натяжение (расталкиваем вершины)
\fmf{heavy,label=$J/\psi$,tension=1/3,
foreground=red+green}{v1,v5}
\fmffreeze
\fmf{gluon,foreground=blue}{v2,v8}
\fmf{gluon,foreground=blue}{v3,v7}
\fmf{gluon,foreground=blue}{v4,v6}
\fmfv{label=$\Gamma_{e^+e^-}$}{v1}
\fmfv{label=$Br_{\text{hadr}}$,label.dist=0.3w}{v5}
\end{fmfgraph*}
\end{fmffile}
При создании диаграммы MetaPost пытается оптимально расположить вершины, минимизируя взвешенную сумму расстояний между ними. При оптимизации используется понятие натяжения между вершинами. По умолчанию натяжение равно 1. С помощью опции tension натяжение можно изменить. Чем меньше натяжение, тем сильнее расталкиваются вершины.
Обычно полученная диаграмма со значениями по умолчанию не требует вмешательства в код. В случае, если результат не устраивает, достаточно, как правило, изменить натяжение для одного, максимум для двух соединений.
Подробнейшую документацию по пакету feynmp можно найти в файле $(TEXMF)/texmf-dist/doc/latex/feynmf/manual.ps.gz, где $(TEXMF) – корень дерева LaTeX (заведомо верно для TeXLive).
Фракталы
META, естественно, поддерживает рекурсию. Пользуясь этим, а также генераторами случайных uniformdeviate и normaldeviate, можно организовать фрактальную «лесопосадку».
%фрактальная лесопосадка beginfig(1) ; u:=1mm; branchrotation := 50; offset := 180-branchrotation; thinning := 0.7; shortening := 0.8; def drawit(expr p, linethickness,col) = draw p withpen pencircle scaled linethickness withcolor col; enddef; %A - основание B - направление роста, n - число бранчей, %size - толщина дерева, col - цвет vardef tree(expr A,B,n,size,col) = save C,D,thickness; pair C,D; thickness := size; C := shortening[B, A rotatedaround(B, offset+uniformdeviate(branchrotation))]; D := shortening[B, A rotatedaround(B, -offset-uniformdeviate(branchrotation))]; if n>0: drawit(A--B, thickness, col); thickness := thinning*thickness; tree(B, C, n-1, thickness,col); tree(B, D, n-1, thickness,col); else: drawit(A--B,thickness,col); thickness := thinning*thickness; drawit(B--C, thickness,col); drawit(B--D, thickness,col); fi; enddef; numeric nbr,nx,ny,ell,size; color col; nx:=10;ny:=5; pair A; for ix:=1 upto nx: for iy:=1 upto ny: nbr:=4+uniformdeviate 5; ell:=nbr*u; x:=ix*(1+1/20*normaldeviate); y:=iy*(1+1/20*normaldeviate); A:=(20u*(x+y*sqrt(2)/2),20u*y*sqrt(2)/2); size:=ell/5; col:=(uniformdeviate 1,uniformdeviate 1,uniformdeviate 1); show ix,iy,A,ell,nbr,size,col; tree(A, A+(0,ell), nbr, size,col); endfor; endfor; endfig;
Увлечение автоматически создаваемыми картинами влечёт за собой опасность переполнения памяти. MetaPost создавался в то время, когда к используемой памяти относились исключительно бережно.
Если при компиляции картинки будет выдана ошибка MetaPost capacity exceeded, то необходимо поправить файл конфигурации texmf.cnf. Обычно этот файл можно найти в директории $(TEXMF)/ web2c/texnf.cnf.
За выделяемый объём памяти для MetaPost отвечает переменная main_memory.mpost. Значение этой переменной должно быть меньше значения main_memory, которое определяет верхнюю границу использования памяти для всех TeX-подобных программ. Обратите внимание на то, что в конфигурационном файле может быть несколько переменных с одним и тем же именем – используется последнее значение.
В моём случае ограничение по памяти составляло 15 Мб. Очевидно, что размер используемой памяти можно безболезненно увеличить. С другой стороны, если происходит переполнение, то это, возможно, значит, что в алгоритм закралась ошибка.
После исправления значения переменных следует заново сгенерировать форматные файлы, например, с помощью команды texconfig init.
Увеличительное стекло
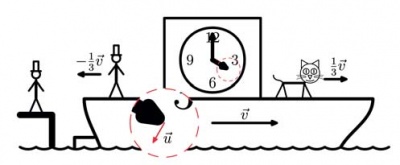
Бывает, в процессе создания картинки необходимо увеличить участок для лучшей детализации. MetaPost предоставляет средство для этого в виде команды clip, которая позволяет обрезать картинку по любому замкнутому пути. Ниже идёт код, который позволил увеличить кусок циферблата корабельных часов.
%Файл dop.mp
R:=3.6u;
path q;
%определяем форму области которую хотим вырезать
q:=(-R,0)..(R,0)..cycle;
%определяем центр вырезаемой области (orig)
%и местоположение увеличенного участка (copy)
pair orig,copy;
orig=(65u,24u);copy=(45u,7.5u);
%отмечаем вырезаемую область
draw q shifted orig dashed evenly scaled 1/2u
withpen pencircle scaled 0.2u witcholor red;
picture p;
%сохраняем текущую картинку в переменной p
p:=currentpicture;
%коэффициент увеличения
numeric scale;scale:=3;
%Обрезаем картинку p по замкнутому пути q
clip p to (q shifted orig);
%чистим область, где будет нарисована увеличенная копия
fill q scaled scale shifted copy withcolor white;
%рисуем копию
draw p shifted -orig scaled scale shifted copy;
%рисуем дополнительную стрелку и метку
%на уже увеличенной копии
draw copy withpen pencircle scaled 1u withcolor red;
drawarrow copy--(copy+7u*dir -120)
withpen pencircle scaled 0.4u withcolor red;
label.lrt(btex \(\vec{u}\) etex,
1/3[copy,(copy+7u*dir -120)]);
Пользуясь этим приёмом, можно создать любой фон для какойугодно фигуры, сделать любую штриховку.
Штриховка
clip-технология, которая упоминалась выше, позволяет создать любой вид штриховки. В стандартной поставке MetaPost идут пакеты, которые этим пользуются.
Пакет hatching.mp представляет из себя обычный «хак»:
%Файл dop.mp
%пример использования пакета hatching
input hatching;
beginfig(3) ;
numeric u;u=1mm;
path q;
q=(10u,0)..{dir -135}(0u,0u){dir 135}..
(-10u,0)..{dir 90}(0u,0u){dir -90}..cycle;
hatchfill q withcolor red withcolor (25,1u,-1);
draw q;
endfig;
Функция hatchfill берёт информацию о штриховке из данных, которые следуют с декларацией withcolor. Сигналом, что эти данные предназначены именно для hatchfill, является то, что голубая компонента тройки чисел меньше 0. Красная компонента соответствует углу наклона штриховки, зелёная – расстоянию между штрихами. Подробности можно узнать в краткой документации к пакету.
Более развитым (возможно, излишне) является пакет mpattern:
%создаём "обои" ракета beginpattern(rocket); begingroup;save u; u:=1mm; draw Rocket scaled 2/3u rotated -30; patternbbox(-5u,-8u,5u,8u); endgroup; endpattern; %создаём "обои" повёрнутая клетка beginpattern(rotated_checker); fill unitsquare scaled 4mm rotated 45 withcolor .7white; endpattern; beginfig(4); numeric u; u:=1mm; path p; z1=(10u,0u); p=fullcircle scaled 50u; %рисуем фигуру в клетку fill p withpattern rotated_checker; unfill p shifted z1; %рисуем фигуру "в ракету" fill p shifted z1 withpattern rocket; endfig;
Здесь уже определены свои команды для создания штриховки. Пакет не свободен от недостатков, но он достаточно прост, и можно легко «довести» код до необходимой кондиции. Простота – это общее свойство пакетов MetaPost. META вынуждает писать кратко. Подробности можно найти в документации к пакету.
Вставка eps
Пакет exteps.mp позволяет включить eps-картинку как единый объект. Краткая документация доступна в файле exteps.pdf, поставляемом с этим пакетом.
%Файл dop.mp input exteps; %Включение eps-картинки beginfig(6) ; numeric u;u:=1mm; % базовая надпись for alpha:=-90 step 3 until 0: label(btex LinuxFormat в России etex scaled (5*(1+alpha/100)) rotated alpha,(0,0)) withcolor (uniformdeviate 1,uniformdeviate 1,uniformdeviate 1); endfor; % посадим Тукса (penguin.eps) справа begineps "penguin.eps" ; % ширина картинки width:=30u; % сдвиг картинки от начала координат base:= (60u,5u); % можно нарисовать решётку на картинки % grid := true; % обрезание по bounding box % clip := true; endeps; % посадим Тукса (penguin.eps) слева begineps "penguin.eps" ; % поворот angle:=90; width:=30u; base:= (-30u,-40u); endeps; endfig ;
Большие числа
Когда обсуждалась вставка меток, в качестве примера был представлен треугольник Паскаля. Из-за ограничений META на максимальный размер числа треугольник Паскаля отрисовывался до 14-й строчки.
Это ограничение можно обойти, воспользовавшись пакетом sarith.mp. Он был создан специально для пакета graphics.mp, что вполне естественно, так как если при рисовании незначительных рисунков больших чисел быть не может, то при анализе данных их наличие – вполне рядовая ситуация.
%Файл dop.mp
%Macros for arithmetic on strings that represent big numbers
input sarith;
%Треугольник Паскаля с большими числами
beginfig(5) ;
numeric u;
u = 1.mm;
numeric dy,dx,x,y,i,j,sy,ds,nlast;dy:=5u;
dx:=6u;x=0;y=0;nlast:=20;
%для хранения больших чисел нужна строка
string n[][];
ds=0.04;sy=0.032;
picture z;
for i:=0 upto nlast:
dy:=dy*(1-sy);
y:=y-dy;
for j:=0 upto i:
if (j=0) or (j=i):
n[i][j]:=Sabs 1; %сложение
else:
n[i][j]:=n[i-1][j-1] Sadd n[i-1][j]; %сложение
fi
%формат вывода
z:=thelabel(format("%6g", n[i][j]),(0,0));
x:=dx*(j-i/2);
label(z scaled (1-ds*i),(x,y));
endfor
z:=thelabel.lft(decimal(i)&":",(0,0));
label(z scaled (1-ds*i),(dx*(-nlast/2-1),y));
endfor
endfig ;
Для представления больших чисел используется встроенный тип string – строка.
| Оператор | Действие |
|---|---|
| Scvnum <number> | конвертация в numric |
| Sabs <number> | абсолютное значение |
| <number> Sadd <number> | сложение |
| <number> Ssub <number> | вычитание |
| <number> Smul <number> | умножение |
| <number> Sdiv <number> | деление |
| <number> Sleq <number> | сравнение <= |
| <number> Sneq <number> | сравнение <> |
Документация к пакету sarith.mp является частью документации к graphics.mp (mpgraph.pdf от Джона Хобби).
Макрос TEX
Вы, наверное, уже обратили внимание, что метки в MetaPost являются статическими. Всё, что между btex и etex, отдаётся LaTeX для обработки. Это значит, что метку нельзя скомпоновать из различных кусков. Решением является немного модифицированный макрос из стандартного пакета TEX.mp:
%Файл macros.mp
vardef TEX primary s =
write "verbatimtex" to "mptextmp.mp";
write "\input{preheader-base}" to "mptextmp.mp";
write "\begin{document}" to "mptextmp.mp";
write "etex" to "mptextmp.mp";
write "btex "&s&" etex" to "mptextmp.mp";
write EOF to "mptextmp.mp";
scantokens "input mptextmp"
enddef;
В процессе вызова макроса TEX всё, что находится внутри него, записывается в mptextmp.mp, а затем этот файл включается в основной файл прямо во время компиляции. То есть происходит модификация программы прямо во время компиляции. Пример использования макроса приведен ниже:
%Файл coord.mp
numeric u;u:=2mm;
for i:=-15 step 5 until 15:
label.lft(TEX("\("&decimal(i)&"\)"),(-10u,i*u));
endfor;
При формировании ASCII-строчки использовался оператор & для объединения. Хотя в данном случае можно было обойтись только статическими записями, но иногда этот приём может пригодиться для целей автоматизации, где скорость компиляции – не главное.
Основной минус этого способа в том, что он очень «мееедленный». Для ускорения следует оставить в preheader-base.tex только самые необходимые инструкции. Что-то вроде:
\documentclass[12pt]{article}
\usepackage[warn]{mathtext}
\usepackage[T2A]{fontenc}
\usepackage[koi8-r]{inputenc}
\usepackage[english,russian]{babel}
Заключение
Естественно, в таком кратком обзоре невозможно рассказать всё. Основные понятия и приёмы уже изложены, но множество вещей выпало из обзора. В частности, совсем не рассмотрены 3D объекты, создание геометрических чертежей, параметризация пути и векторные поля в MetaPost. Это не смертельно, так как есть весьма качественная свободная литература, посвящённая этим предметам.
MetaPost достаточно легко использовать после обучения, но обучение перед использованием просто необходимо. Это свойство всех стоящих технологий, которые позволяют делать то, для чего компьютеры и существуют: автоматизировать рутинные действия, для выполнения которых не требуется задумываться. Думать же, в любом случае, прерогатива человека.