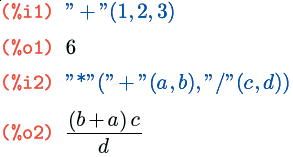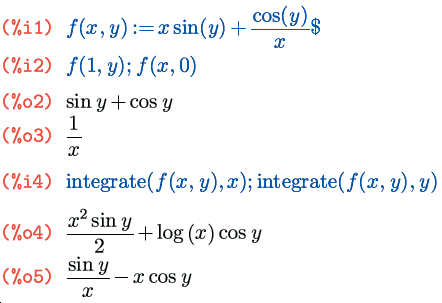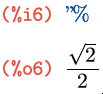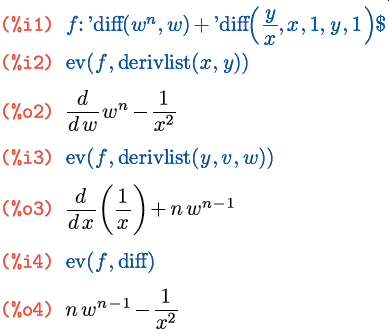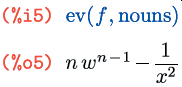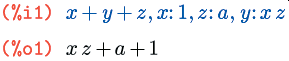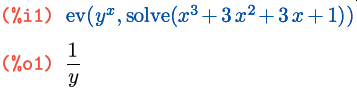Журнал LinuxFormat - перейти на главную

LXF82:Maxima

Материал из Linuxformat
(Различия между версиями)
Перейти к: навигация, поиск
(Новая: {{Цикл/Maxima}} == Maxima – функции и операторы == ''ЧАСТЬ 2 Понять философию сложного пакета – уже половина дел...)
 
(иллюстрация)
 
(не показана 1 промежуточная версия 1 участника)
Строка 1: Строка 1:
 
{{Цикл/Maxima}}
 
{{Цикл/Maxima}}
−
== Maxima – функции и операторы ==
+
== Maxima — функции и операторы ==
−
''ЧАСТЬ 2 Понять философию сложного пакета – уже половина дела, однако, для того, чтобы уметь читать, надо хотя бы освоить азбуку. Сегодня '''Тихон Тарнавский''' расскажет вам об операторах (или функциях?) Maxima.''
+
''ЧАСТЬ 2 Понять философию сложного пакета — уже половина дела, однако, для того, чтобы уметь читать, надо хотя бы освоить азбуку. Сегодня '''Тихон Тарнавский''' расскажет вам об операторах (или функциях?) Maxima.''
  
 
=== Операторы Максимы ===
 
=== Операторы Максимы ===
Строка 8: Строка 8:
 
свойствах.
 
свойствах.
  
−
На самом деле в Максиме нет чёткого разграничения между операторами и функциями. Более того, каждый оператор – это на самом деле
+
На самом деле в Максиме нет чёткого разграничения между операторами и функциями. Более того, каждый оператор — это на самом деле
 
функция:
 
функция:
−
 
+
[[Изображение:Img 82 106 1.png|center]]
  
 
Здесь имена функций-операторов берутся в кавычки лишь потому,
 
Здесь имена функций-операторов берутся в кавычки лишь потому,
 
что содержат символы, нестандартные для имён функций. Это похоже на
 
что содержат символы, нестандартные для имён функций. Это похоже на
 
работу в командной оболочке Unix, где, если в имя файла входят управляющие символы, вы можете либо взять это имя в кавычки, либо экранировать каждый такой символ обратным слэшем. В Maxima допустимы те же
 
работу в командной оболочке Unix, где, если в имя файла входят управляющие символы, вы можете либо взять это имя в кавычки, либо экранировать каждый такой символ обратным слэшем. В Maxima допустимы те же
−
два варианта: например, вместо “+” можно было бы написать \+.
+
два варианта: например, вместо «+» можно было бы написать \+.
  
 
Итак, все встроенные операторы максимы являются функциями;
 
Итак, все встроенные операторы максимы являются функциями;
Строка 26: Строка 26:
 
некоторых операторах, но и о нескольких функциях, которые по природе
 
некоторых операторах, но и о нескольких функциях, которые по природе
 
своих действий сходны с операторами. Наиболее привычные операторы
 
своих действий сходны с операторами. Наиболее привычные операторы
−
уже упоминались в предыдущей статье: +, –, *, /, ^ или ** (возведение
+
уже упоминались в предыдущей статье: +, -, *, /, ^ или ** (возведение
 
в степень) и функцию sqrt(x) (квадратный корень). Сегодня мы поговорим ещё о нескольких достаточно распространённых.
 
в степень) и функцию sqrt(x) (квадратный корень). Сегодня мы поговорим ещё о нескольких достаточно распространённых.
  
 
Точкой обозначается матричное произведение. В документации
 
Точкой обозначается матричное произведение. В документации
−
утверждается, что сама точка при этом должна быть отделена пробелами от обоих своих операндов – дабы не спутать её с точкой десятичной.
+
утверждается, что сама точка при этом должна быть отделена пробелами от обоих своих операндов — дабы не спутать её с точкой десятичной.
 
На самом деле мне не удалось добиться от Максимы неадекватной реакции и в «беспробельном» варианте; что и логично, так как всё равно эти
 
На самом деле мне не удалось добиться от Максимы неадекватной реакции и в «беспробельном» варианте; что и логично, так как всё равно эти
 
две разные ипостаси точки можно различить по контексту: ведь цифры
 
две разные ипостаси точки можно различить по контексту: ведь цифры
 
именами матриц быть не могут. Так что, думаю, можете смело писать и
 
именами матриц быть не могут. Так что, думаю, можете смело писать и
 
без пробелов.
 
без пробелов.
−
 
+
[[Изображение:Img 82 106 2.png|center]]
  
 
В случае, если заданные матрицы не могут быть перемножены из-за
 
В случае, если заданные матрицы не могут быть перемножены из-за
 
несовпадающих размерностей, Maxima выдаст сообщение об ошибке:
 
несовпадающих размерностей, Maxima выдаст сообщение об ошибке:
 +
[[Изображение:Img 82 106 3.png|center]]
  
−
 
+
Восклицательный знак, стоящий после своего аргумента (то есть постфиксный оператор), традиционно обозначает факториал. Не менее традиционно, двумя восклицательными знаками обозначен полуфакториал
−
Восклицательный знак, стоящий после своего аргумента (т.е. постфиксный оператор), традиционно обозначает факториал. Не менее традиционно, двумя восклицательными знаками обозначен полуфакториал
+
 
[произведение всех четных (для четного операнда) или нечетных чисел,
 
[произведение всех четных (для четного операнда) или нечетных чисел,
−
меньших либо равных данному, – прим. ред.]. Функции abs(x) и
+
меньших либо равных данному, — прим. ред.]. Функции abs(x) и
 
signum(x) возвращают, как опять же нетрудно догадаться, модуль и
 
signum(x) возвращают, как опять же нетрудно догадаться, модуль и
−
знак числа. А функции max(x1,...,xn) и min(x1,...,xn) – соответственно максимальное и минимальное из заданных чисел.
+
знак числа. А функции max(x1,…,xn) и min(x1,…,xn) — соответственно максимальное и минимальное из заданных чисел.
−
 
+
  
 
Тут стоит остановиться на нескольких моментах. Во-первых, все
 
Тут стоит остановиться на нескольких моментах. Во-первых, все
Строка 52: Строка 51:
 
но и комплексными числами. Сами комплексные числа записываются в
 
но и комплексными числами. Сами комплексные числа записываются в
 
Максиме в алгебраической форме, с мнимой единицей, обозначенной
 
Максиме в алгебраической форме, с мнимой единицей, обозначенной
−
через %i; то есть в виде a+b*%i, где a и b – соответственно действительная и мнимая части числа.
+
через %i; то есть в виде a+b*%i, где a и b — соответственно действительная и мнимая части числа.
  
 
Так, факториал задан в наиболее общем виде и представляет собой,
 
Так, факториал задан в наиболее общем виде и представляет собой,
Строка 59: Строка 58:
 
При этом факториал от натурального числа (и нуля) автоматически
 
При этом факториал от натурального числа (и нуля) автоматически
 
упрощается до натурального же числа:
 
упрощается до натурального же числа:
−
 
+
[[Изображение:Img 82 107 1.png|center]]
  
 
Точно так же и модуль определён для всех комплексных чисел
 
Точно так же и модуль определён для всех комплексных чисел
−
(напомню, что |a+b*i|=sqrt(a2+b2)). Минимум, максимум и знак определены, естественным образом, только для действительных чисел, так как
+
(напомню, что <math>|a+b*i|=sqrt(a^2+b^2)</math>). Минимум, максимум и знак определены, естественным образом, только для действительных чисел, так как
 
комплексные числа общего вида, как известно, между собой
 
комплексные числа общего вида, как известно, между собой
 
несравнимы.
 
несравнимы.
  
 
Второй важный момент: когда некоторая встроенная функция или
 
Второй важный момент: когда некоторая встроенная функция или
−
оператор Maxima не может получить для переданного выражения однозначный результат (ввиду недостаточности данных) – она пытается максимально упростить это выражение. (Для некоторых функций такое
+
оператор Maxima не может получить для переданного выражения однозначный результат (ввиду недостаточности данных) — она пытается максимально упростить это выражение. (Для некоторых функций такое
 
автоупрощение регулируется специальными параметрами.) Например,
 
автоупрощение регулируется специальными параметрами.) Например,
 
если x не задан:
 
если x не задан:
−
 
+
[[Изображение:Img 82 107 2.png|center]]
  
 
Подобные упрощения, равно как и «раскрытие» факториалов и
 
Подобные упрощения, равно как и «раскрытие» факториалов и
 
арифметических операторов, не считаются вычислениями, а следовательно оператор блокировки вычислений их не предотвращает:
 
арифметических операторов, не считаются вычислениями, а следовательно оператор блокировки вычислений их не предотвращает:
−
 
+
[[Изображение:Img 82 107 3.png|center]]
  
 
Как вы, вероятно, помните, в прошлый раз кроме упомянутого только что оператора блокировки вычислений мы познакомились с оператором присвоения значений, или, иначе, именования выражений, : . В
 
Как вы, вероятно, помните, в прошлый раз кроме упомянутого только что оператора блокировки вычислений мы познакомились с оператором присвоения значений, или, иначе, именования выражений, : . В
 
Maxima существуют и другие операторы именования, из которых нам на
 
Maxima существуют и другие операторы именования, из которых нам на
−
данный момент интересен один – оператор задания функции.
+
данный момент интересен один — оператор задания функции.
 
Обозначается он через :=, и аналогии здесь прослеживаются не с языками Pascal или Algol, как может показаться на первый взгляд, а с другими обозначениями самой Максимы: с одной стороны определение
 
Обозначается он через :=, и аналогии здесь прослеживаются не с языками Pascal или Algol, как может показаться на первый взгляд, а с другими обозначениями самой Максимы: с одной стороны определение
−
функции можно воспринимать как уравнение (которое обозначается знаком =), а с другой – оно родственно назначению имени некоторому
+
функции можно воспринимать как уравнение (которое обозначается знаком =), а с другой — оно родственно назначению имени некоторому
 
выражению (то есть :). То есть определение функции можно в какой-то
 
выражению (то есть :). То есть определение функции можно в какой-то
−
мере считать симбиозом этих двух выражений – и оттого вполне логично, что оно обозначается обоими их символами. (В продолжение этой
+
мере считать симбиозом этих двух выражений — и оттого вполне логично, что оно обозначается обоими их символами. (В продолжение этой
 
аналогии могу добавить, что в Maxima есть и расширенные варианты
 
аналогии могу добавить, что в Maxima есть и расширенные варианты
 
операторов присвоения и назначения функции, обозначаемые соответственно через :: и ::=.)
 
операторов присвоения и назначения функции, обозначаемые соответственно через :: и ::=.)
−
 
+
[[Изображение:Img 82 107 4.png|center]]
  
 
Думаю, основы работы с функциями самоочевидны по аналогии с
 
Думаю, основы работы с функциями самоочевидны по аналогии с
Строка 93: Строка 92:
 
А сейчас я расскажу о том, что было обещано в прошлый раз: о возможностях управлять процессом вычислений вводимых вами выражений. В
 
А сейчас я расскажу о том, что было обещано в прошлый раз: о возможностях управлять процессом вычислений вводимых вами выражений. В
 
прошлый раз, о чём я уже вспоминал, было упомянуто только одно такое
 
прошлый раз, о чём я уже вспоминал, было упомянуто только одно такое
−
средство – блокировка вычислений. Здесь всё достаточно просто и дополнительно стоит остановиться только на одном моменте. Если апострофом
+
средство — блокировка вычислений. Здесь всё достаточно просто и дополнительно стоит остановиться только на одном моменте. Если апострофом
−
предварён вызов функции (встроенной ли, пользовательской – несущественно), то блокируется вычисление самой функции, но не её аргументов.
+
предварён вызов функции (встроенной ли, пользовательской — несущественно), то блокируется вычисление самой функции, но не её аргументов.
 
Если же поставить апостроф перед выражением, заключённым в скобки,
 
Если же поставить апостроф перед выражением, заключённым в скобки,
−
то невычисленными останется всё это выражение целиком, т.е. и все входящие в него функции, и все аргументы этих функций. Например:
+
то невычисленными останется всё это выражение целиком, то есть и все входящие в него функции, и все аргументы этих функций. Например:
−
 
+
[[Изображение:Img 82 109 1.png|center]]
  
 
В противовес блокировке вычислений, можно также принудительно
 
В противовес блокировке вычислений, можно также принудительно
−
вычислить любое выражение – для этого тоже существует оператор,
+
вычислить любое выражение — для этого тоже существует оператор,
 
состоящий из двух апострофов:
 
состоящий из двух апострофов:
 +
[[Изображение:Img 82 109 2.png|center]]
  
−
 
+
В терминологии Maxima невычисленная форма выражения называется «noun form», вычисленная — «verb form». Сохраняя лингвистические параллели, на русский я бы это перевёл как «несовершённая форма» и «совершённая форма».
−
В терминологии Maxima невычисленная форма выражения называется «noun form», вычисленная – «verb form». Сохраняя лингвистические параллели, на русский я бы это перевёл как «несовершённая форма» и «совершённая форма».
+
  
 
Если говорить о ячейках ввода-вывода, то значение ячейки ввода в
 
Если говорить о ячейках ввода-вывода, то значение ячейки ввода в
−
Maxima закономерно сохраняется до его вычисления (т.е. в несовершённой форме), а значение ячейки вывода – после (т.е. в совершённой);
+
Maxima закономерно сохраняется до его вычисления (то есть в несовершённой форме), а значение ячейки вывода — после (то есть в совершённой);
−
другими словами, тут сохраняется естественный порядок «ввод –>
+
другими словами, тут сохраняется естественный порядок «ввод ->
−
вычисление –> вывод».
+
вычисление -> вывод».
−
 
+
[[Изображение:Img 82 109 3.png|center]]
  
 
Как видите, операторы вычисления и блокировки вычислений имеют накопительный эффект. О другой стороне этого эффекта мы поговорим чуть ниже.
 
Как видите, операторы вычисления и блокировки вычислений имеют накопительный эффект. О другой стороне этого эффекта мы поговорим чуть ниже.
Строка 117: Строка 116:
 
к функции ev(выражение). Сама функция ev предоставляет гораздо
 
к функции ev(выражение). Сама функция ev предоставляет гораздо
 
более широкие возможности, нежели простое принудительное вычисление заданного выражения: она может принимать произвольное число
 
более широкие возможности, нежели простое принудительное вычисление заданного выражения: она может принимать произвольное число
−
аргументов, первый из которых – вычисляемое выражение, а остальные
+
аргументов, первый из которых — вычисляемое выражение, а остальные
−
– специальные опции, которые как раз и влияют на то, как именно будет
+
— специальные опции, которые как раз и влияют на то, как именно будет
−
производиться вычисление. Точно так же, как двойной апостроф –
+
производиться вычисление. Точно так же, как двойной апостроф -
 
сокращение для ev без дополнительных опций, есть ещё более упрощённая запись функции ev с опциями: в этом случае вместо имени функции
 
сокращение для ev без дополнительных опций, есть ещё более упрощённая запись функции ev с опциями: в этом случае вместо имени функции
−
и скобок вообще ничего писать не нужно; т.е. «ev(выражение, опц1,опц2, ...)» можно записать просто как «выражение, опц1, опц2,
+
и скобок вообще ничего писать не нужно; то есть «ev(выражение, опц1,опц2, …)» можно записать просто как «выражение, опц1, опц2,
−
...».
+
…».
  
−
Первая из таких опций связана с автоупрощением. Глобально автоупрощение регулируется переключателем simp (от «simplification» –
+
Первая из таких опций связана с автоупрощением. Глобально автоупрощение регулируется переключателем simp (от «simplification» -
 
упрощение), и по умолчанию оно включено; в любой момент его можно
 
упрощение), и по умолчанию оно включено; в любой момент его можно
 
выключить, установив значение переключателя в false. Опция функции
 
выключить, установив значение переключателя в false. Опция функции
 
ev, одноимённая этому переключателю, позволяет включить упрощение
 
ev, одноимённая этому переключателю, позволяет включить упрощение
−
для данного конкретного вычисления – вне зависимости от того, включено или выключено оно глобально:
+
для данного конкретного вычисления — вне зависимости от того, включено или выключено оно глобально:
−
 
+
[[Изображение:Img 82 110 1.png|center]]
  
 
Тут нужно отметить ещё, что вызов kill(all) не восстанавливает
 
Тут нужно отметить ещё, что вызов kill(all) не восстанавливает
−
умолчательные значения переключателей; т.е. если мы, к примеру,
+
умолчательные значения переключателей; то есть если мы, к примеру,
 
изменили значение переключателя simp, как в примере выше, то для
 
изменили значение переключателя simp, как в примере выше, то для
 
того, чтобы вернуться к изначальному порядку вещей, установленному
 
того, чтобы вернуться к изначальному порядку вещей, установленному
Строка 139: Строка 138:
  
 
Опция diff принудительно раскрывает все производные и полные
 
Опция diff принудительно раскрывает все производные и полные
−
дифференциалы; а опция derivlist(x, y, ..., v) – производные относительно переменных, заданных в качестве её аргументов, а также полные
+
дифференциалы; а опция derivlist(x, y, …, v) — производные относительно переменных, заданных в качестве её аргументов, а также полные
 
дифференциалы (так как они не зависят ни от каких переменных):
 
дифференциалы (так как они не зависят ни от каких переменных):
−
 
+
[[Изображение:Img 82 110 2.png|center]]
  
 
Как видите, если из нескольких переменных из diff в derivlist()
 
Как видите, если из нескольких переменных из diff в derivlist()
−
заданы не все, то раскрывается производная только по заданным переменным; это и понятно, так как выражения diff(f, x, 1, y, 1), diff(diff(f,x), y) и diff(diff(f, y), x) математически эквивалентны [по крайней
+
заданы не все, то раскрывается производная только по заданным переменным; это и понятно, так как выражения diff(f, x, 1, y, 1), diff(diff(f, x), y) и diff(diff(f, y), x) математически эквивалентны [по крайней
−
мере, для «хороших» функций, – прим.ред]. Если же аргумент опции
+
мере, для «хороших» функций, — прим.ред]. Если же аргумент опции
 
derivlist() вообще не является переменной дифференцирования, он
 
derivlist() вообще не является переменной дифференцирования, он
 
просто игнорируется.
 
просто игнорируется.
  
−
Опция nouns раскрывает вообще все несовершённые формы – и
+
Опция nouns раскрывает вообще все несовершённые формы — и
 
производные в том числе:
 
производные в том числе:
−
 
+
[[Изображение:Img 82 110 3.png|center]]
  
 
Опция float преобразовывает все рациональные числа в конечную
 
Опция float преобразовывает все рациональные числа в конечную
 
десятичную запись; опция numer включает опцию float и, кроме того,
 
десятичную запись; опция numer включает опцию float и, кроме того,
 
приводит к десятичному виду многие математические функции от числовых аргументов:
 
приводит к десятичному виду многие математические функции от числовых аргументов:
 +
[[Изображение:Img 82 110 4.png|center]]
  
−
 
+
Опция noeval блокирует сам этап вычисления как таковой; то есть её
−
Опция noeval блокирует сам этап вычисления как таковой; т.е. её
+
 
можно использовать для того, чтобы применить к выражению другие
 
можно использовать для того, чтобы применить к выражению другие
 
опции функции ev, не перевычисляя его. При этом опять-таки нужно
 
опции функции ev, не перевычисляя его. При этом опять-таки нужно
 
понимать разницу между вычислением и упрощением:
 
понимать разницу между вычислением и упрощением:
−
 
+
[[Изображение:Img 82 110 5.png|center]]
  
 
Таким образом, мы можем принудительно упростить выражение, не
 
Таким образом, мы можем принудительно упростить выражение, не
 
перевычисляя его.
 
перевычисляя его.
  
−
Опция eval – напротив, проводит дополнительно ещё один процесс
+
Опция eval — напротив, проводит дополнительно ещё один процесс
 
вычисления. Здесь стоит поговорить подробнее о накопительном
 
вычисления. Здесь стоит поговорить подробнее о накопительном
 
эффекте вычисления, который я уже демонстрировал выше. Так как в
 
эффекте вычисления, который я уже демонстрировал выше. Так как в
Строка 175: Строка 174:
 
значений» может продолжаться сколь угодно глубоко. Один вызов функции ev (без опции eval) опускается по этой цепочке в глубину на один
 
значений» может продолжаться сколь угодно глубоко. Один вызов функции ev (без опции eval) опускается по этой цепочке в глубину на один
 
уровень:
 
уровень:
−
 
+
[[Изображение:Img 82 110 6.png|center]]
  
 
Напомню, что здесь ev(y), eval является сокращённой записью от
 
Напомню, что здесь ev(y), eval является сокращённой записью от
 
ev(ev(y), eval), таким образом вычисление в этом выражении проводится трижды. Кроме того, хочу обратить ваше внимание на порядок
 
ev(ev(y), eval), таким образом вычисление в этом выражении проводится трижды. Кроме того, хочу обратить ваше внимание на порядок
 
назначения выражений символам; здесь существенно, что на момент
 
назначения выражений символам; здесь существенно, что на момент
−
задания каждого выражения входящий в него символ ещё не был определён – иначе в выражение автоматически подставлялся не сам символ,
+
задания каждого выражения входящий в него символ ещё не был определён — иначе в выражение автоматически подставлялся не сам символ,
−
а его значение. Таким образом, если бы мы произвели эти же назначения в обратном порядке, то значением символа y стало бы xm+6 – безо
+
а его значение. Таким образом, если бы мы произвели эти же назначения в обратном порядке, то значением символа y стало бы xm+6 — безо
 
всяких принудительных вычислений.
 
всяких принудительных вычислений.
  
Строка 189: Строка 188:
 
можно использовать и для того, чтобы разблокировать блокировку
 
можно использовать и для того, чтобы разблокировать блокировку
 
вычислений любой глубины вложения:
 
вычислений любой глубины вложения:
−
 
+
[[Изображение:Img 82 111 1.png|center]]
  
 
В других ситуациях использовать этот переключатель следует с
 
В других ситуациях использовать этот переключатель следует с
Строка 199: Строка 198:
  
 
Кроме константных значений есть ещё несколько видов опций.
 
Кроме константных значений есть ещё несколько видов опций.
−
Первый из них – это имена специальных функций, которые занимаются
+
Первый из них — это имена специальных функций, которые занимаются
 
упрощением или преобразованием математических выражений. Будучи
 
упрощением или преобразованием математических выражений. Будучи
−
упомянута по имени в качестве опции, такая функция просто применяется к вычисляемому выражению. Например, выражение, fullratsimp –
+
упомянута по имени в качестве опции, такая функция просто применяется к вычисляемому выражению. Например, выражение, fullratsimp -
 
это то же самое, что и fullratsimp(ev(выражение)). Полный список
 
это то же самое, что и fullratsimp(ev(выражение)). Полный список
 
таких функций вы можете найти в ? evfun.
 
таких функций вы можете найти в ? evfun.
  
 
Если в качестве опции ввести имя любой другой функции, не имеющей свойства evfun, то все несовершённые вхождения этой функции
 
Если в качестве опции ввести имя любой другой функции, не имеющей свойства evfun, то все несовершённые вхождения этой функции
−
будут заменены совершёнными, т.е. принудительно вычислены.
+
будут заменены совершёнными, то есть принудительно вычислены.
  
 
{{Врезка
 
{{Врезка
Строка 218: Строка 217:
 
|Ширина=250px}}
 
|Ширина=250px}}
 
Также в качестве опции можно задать назначение символа или функции; все такие назначения действуют локально в пределах вычисляемого выражения, и все подстановки производятся параллельно:
 
Также в качестве опции можно задать назначение символа или функции; все такие назначения действуют локально в пределах вычисляемого выражения, и все подстановки производятся параллельно:
 +
[[Изображение:Img 82 111 2.png|center]]
  
 
Опция подстановки символа допустима не только в виде оператора
 
Опция подстановки символа допустима не только в виде оператора
 
присвоения, но и в виде равенства; сделано это, в частности, для того,
 
присвоения, но и в виде равенства; сделано это, в частности, для того,
 
чтобы в качестве подстановок можно было использовать решения, найденные функцией solve:
 
чтобы в качестве подстановок можно было использовать решения, найденные функцией solve:
−
 
+
[[Изображение:Img 82 111 3.png|center]]
  
 
Вот и всё на сегодня. В следующий раз мы начнём с уже упомянутых вскользь функций по упрощению и преобразованию выражений.
 
Вот и всё на сегодня. В следующий раз мы начнём с уже упомянутых вскользь функций по упрощению и преобразованию выражений.
Строка 256: Строка 256:
 
которых я сейчас и расскажу.
 
которых я сейчас и расскажу.
  
 +
[[Изображение:Img 82 108 1.png|thumb|Рисунок 1. Консольная Maxima.]]
 
Начнём с консольного интерфейса, доступного по команде Maxima;
 
Начнём с консольного интерфейса, доступного по команде Maxima;
 
он выполнен в традиционном стиле командной строки: на экране чередуются вводимые вами команды и ответы системы на них (рис. 1).
 
он выполнен в традиционном стиле командной строки: на экране чередуются вводимые вами команды и ответы системы на них (рис. 1).
Строка 266: Строка 267:
 
из графических интерфейсов. Единственный реальный плюс консольного интерфейса – это минимальные требования к ресурсам. В остальном всё, как видите, довольно аскетично.
 
из графических интерфейсов. Единственный реальный плюс консольного интерфейса – это минимальные требования к ресурсам. В остальном всё, как видите, довольно аскетично.
  
 +
[[Изображение:Img 82 108 2.png|thumb|left|Рисунок 2. Xmaxima.]]
 
Самый примитивный из графических интерфейсов, – XMaxima
 
Самый примитивный из графических интерфейсов, – XMaxima
 
(рис. 2). На иллюстрации верхняя половина окна – это собственно рабочая область, нижняя – помощь. Кроме этого отдельного окна помощи
 
(рис. 2). На иллюстрации верхняя половина окна – это собственно рабочая область, нижняя – помощь. Кроме этого отдельного окна помощи
Строка 271: Строка 273:
 
если тот запущен в X. Посему и тут долго задерживаться не будем.
 
если тот запущен в X. Посему и тут долго задерживаться не будем.
  
 +
[[Изображение:Img 82 108 3.png|thumb|Рисунок 3. Maxima-Emacs.]]
 
А рассмотрим следующий интерфейс – Maxima-Emacs. Он, как
 
А рассмотрим следующий интерфейс – Maxima-Emacs. Он, как
 
нетрудно догадаться, запускает сессию Максимы в буфере широко
 
нетрудно догадаться, запускает сессию Максимы в буфере широко
Строка 287: Строка 290:
 
взаимодействии ещё с одним интерфейсом, о котором чуть ниже.
 
взаимодействии ещё с одним интерфейсом, о котором чуть ниже.
  
 +
[[Изображение:Img 82 109 4.png|thumb|left|Рисунок 4. Ячейка Максимы введенная и вычисленная в Emacs-режиме Emaxima.]]
 
Следующие два интерфейса – EMaxima и iMaxima – также являются режимами редактора Emacs. Первый – скорее не самостоятельный
 
Следующие два интерфейса – EMaxima и iMaxima – также являются режимами редактора Emacs. Первый – скорее не самостоятельный
 
режим, а надстройка над режимом LaTeX, которая наверняка понравится тем, кто использует Emacs для редактирования LaTeX-документов. В отличие от режима Maxima, который предназначен для обычного изолированного запуска полноценной Maxima-сессии, здесь речь
 
режим, а надстройка над режимом LaTeX, которая наверняка понравится тем, кто использует Emacs для редактирования LaTeX-документов. В отличие от режима Maxima, который предназначен для обычного изолированного запуска полноценной Maxima-сессии, здесь речь

Текущая версия на 13:28, 30 декабря 2008

Подписка на печатную версию
Весь 2015 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)
Подписка на электронную версию
Весь 2015 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)
Подшивки старых номеров журнала (печатные версии)
Весь 2014 год (12 номеров)
Первое полугодие (6 номеров)
Второе полугодие (6 номеров)

[править] Maxima — функции и операторы

ЧАСТЬ 2 Понять философию сложного пакета — уже половина дела, однако, для того, чтобы уметь читать, надо хотя бы освоить азбуку. Сегодня Тихон Тарнавский расскажет вам об операторах (или функциях?) Maxima.

[править] Операторы Максимы

Продолжаю знакомить вас с возможностями свободной программы символьных вычислений Maxima. Начну в этот раз с краткого рассказа об основных операторах Maxima и некоторых их свойствах.

На самом деле в Максиме нет чёткого разграничения между операторами и функциями. Более того, каждый оператор — это на самом деле функция:

Img 82 106 1.png

Здесь имена функций-операторов берутся в кавычки лишь потому, что содержат символы, нестандартные для имён функций. Это похоже на работу в командной оболочке Unix, где, если в имя файла входят управляющие символы, вы можете либо взять это имя в кавычки, либо экранировать каждый такой символ обратным слэшем. В Maxima допустимы те же два варианта: например, вместо «+» можно было бы написать \+.

Итак, все встроенные операторы максимы являются функциями; более того, вы можете наделить любую (в том числе свою собственную) функцию определёнными свойствами, которые фактически превратят её в оператор. Подробнее об этом я расскажу в следующих выпусках.

Таким образом, разделение на функции и операторы в Maxima достаточно условно. Посему в этом разделе речь пойдёт не только о некоторых операторах, но и о нескольких функциях, которые по природе своих действий сходны с операторами. Наиболее привычные операторы уже упоминались в предыдущей статье: +, -, *, /, ^ или ** (возведение в степень) и функцию sqrt(x) (квадратный корень). Сегодня мы поговорим ещё о нескольких достаточно распространённых.

Точкой обозначается матричное произведение. В документации утверждается, что сама точка при этом должна быть отделена пробелами от обоих своих операндов — дабы не спутать её с точкой десятичной. На самом деле мне не удалось добиться от Максимы неадекватной реакции и в «беспробельном» варианте; что и логично, так как всё равно эти две разные ипостаси точки можно различить по контексту: ведь цифры именами матриц быть не могут. Так что, думаю, можете смело писать и без пробелов.

Img 82 106 2.png

В случае, если заданные матрицы не могут быть перемножены из-за несовпадающих размерностей, Maxima выдаст сообщение об ошибке:

Img 82 106 3.png

Восклицательный знак, стоящий после своего аргумента (то есть постфиксный оператор), традиционно обозначает факториал. Не менее традиционно, двумя восклицательными знаками обозначен полуфакториал [произведение всех четных (для четного операнда) или нечетных чисел, меньших либо равных данному, — прим. ред.]. Функции abs(x) и signum(x) возвращают, как опять же нетрудно догадаться, модуль и знак числа. А функции max(x1,…,xn) и min(x1,…,xn) — соответственно максимальное и минимальное из заданных чисел.

Тут стоит остановиться на нескольких моментах. Во-первых, все функции и операторы Maxima работают не только с действительными, но и комплексными числами. Сами комплексные числа записываются в Максиме в алгебраической форме, с мнимой единицей, обозначенной через %i; то есть в виде a+b*%i, где a и b — соответственно действительная и мнимая части числа.

Так, факториал задан в наиболее общем виде и представляет собой, по сути, гамма-функцию (точнее, x! = gamma(x+1)), то есть определён на множестве всех комплексных чисел, кроме отрицательных целых. При этом факториал от натурального числа (и нуля) автоматически упрощается до натурального же числа:

Img 82 107 1.png

Точно так же и модуль определён для всех комплексных чисел (напомню, что <math>|a+b*i|=sqrt(a^2+b^2)</math>). Минимум, максимум и знак определены, естественным образом, только для действительных чисел, так как комплексные числа общего вида, как известно, между собой несравнимы.

Второй важный момент: когда некоторая встроенная функция или оператор Maxima не может получить для переданного выражения однозначный результат (ввиду недостаточности данных) — она пытается максимально упростить это выражение. (Для некоторых функций такое автоупрощение регулируется специальными параметрами.) Например, если x не задан:

Img 82 107 2.png

Подобные упрощения, равно как и «раскрытие» факториалов и арифметических операторов, не считаются вычислениями, а следовательно оператор блокировки вычислений их не предотвращает:

Img 82 107 3.png

Как вы, вероятно, помните, в прошлый раз кроме упомянутого только что оператора блокировки вычислений мы познакомились с оператором присвоения значений, или, иначе, именования выражений, : . В Maxima существуют и другие операторы именования, из которых нам на данный момент интересен один — оператор задания функции. Обозначается он через :=, и аналогии здесь прослеживаются не с языками Pascal или Algol, как может показаться на первый взгляд, а с другими обозначениями самой Максимы: с одной стороны определение функции можно воспринимать как уравнение (которое обозначается знаком =), а с другой — оно родственно назначению имени некоторому выражению (то есть :). То есть определение функции можно в какой-то мере считать симбиозом этих двух выражений — и оттого вполне логично, что оно обозначается обоими их символами. (В продолжение этой аналогии могу добавить, что в Maxima есть и расширенные варианты операторов присвоения и назначения функции, обозначаемые соответственно через :: и ::=.)

Img 82 107 4.png

Думаю, основы работы с функциями самоочевидны по аналогии с приведенным примером, а подробнее об этом мы поговорим в следующих выпусках.

[править] Функция вычисления всего

А сейчас я расскажу о том, что было обещано в прошлый раз: о возможностях управлять процессом вычислений вводимых вами выражений. В прошлый раз, о чём я уже вспоминал, было упомянуто только одно такое средство — блокировка вычислений. Здесь всё достаточно просто и дополнительно стоит остановиться только на одном моменте. Если апострофом предварён вызов функции (встроенной ли, пользовательской — несущественно), то блокируется вычисление самой функции, но не её аргументов. Если же поставить апостроф перед выражением, заключённым в скобки, то невычисленными останется всё это выражение целиком, то есть и все входящие в него функции, и все аргументы этих функций. Например:

Img 82 109 1.png

В противовес блокировке вычислений, можно также принудительно вычислить любое выражение — для этого тоже существует оператор, состоящий из двух апострофов:

Img 82 109 2.png

В терминологии Maxima невычисленная форма выражения называется «noun form», вычисленная — «verb form». Сохраняя лингвистические параллели, на русский я бы это перевёл как «несовершённая форма» и «совершённая форма».

Если говорить о ячейках ввода-вывода, то значение ячейки ввода в Maxima закономерно сохраняется до его вычисления (то есть в несовершённой форме), а значение ячейки вывода — после (то есть в совершённой); другими словами, тут сохраняется естественный порядок «ввод -> вычисление -> вывод».

Img 82 109 3.png

Как видите, операторы вычисления и блокировки вычислений имеют накопительный эффект. О другой стороне этого эффекта мы поговорим чуть ниже.

Оператор, обозначенный двумя апострофами, является синонимом к функции ev(выражение). Сама функция ev предоставляет гораздо более широкие возможности, нежели простое принудительное вычисление заданного выражения: она может принимать произвольное число аргументов, первый из которых — вычисляемое выражение, а остальные — специальные опции, которые как раз и влияют на то, как именно будет производиться вычисление. Точно так же, как двойной апостроф - сокращение для ev без дополнительных опций, есть ещё более упрощённая запись функции ev с опциями: в этом случае вместо имени функции и скобок вообще ничего писать не нужно; то есть «ev(выражение, опц1,опц2, …)» можно записать просто как «выражение, опц1, опц2, …».

Первая из таких опций связана с автоупрощением. Глобально автоупрощение регулируется переключателем simp (от «simplification» - упрощение), и по умолчанию оно включено; в любой момент его можно выключить, установив значение переключателя в false. Опция функции ev, одноимённая этому переключателю, позволяет включить упрощение для данного конкретного вычисления — вне зависимости от того, включено или выключено оно глобально:

Img 82 110 1.png

Тут нужно отметить ещё, что вызов kill(all) не восстанавливает умолчательные значения переключателей; то есть если мы, к примеру, изменили значение переключателя simp, как в примере выше, то для того, чтобы вернуться к изначальному порядку вещей, установленному сразу после запуска Maxima, нам нужно не только сделать kill(all), но и вручную назначить simp:true.

Опция diff принудительно раскрывает все производные и полные дифференциалы; а опция derivlist(x, y, …, v) — производные относительно переменных, заданных в качестве её аргументов, а также полные дифференциалы (так как они не зависят ни от каких переменных):

Img 82 110 2.png

Как видите, если из нескольких переменных из diff в derivlist() заданы не все, то раскрывается производная только по заданным переменным; это и понятно, так как выражения diff(f, x, 1, y, 1), diff(diff(f, x), y) и diff(diff(f, y), x) математически эквивалентны [по крайней мере, для «хороших» функций, — прим.ред]. Если же аргумент опции derivlist() вообще не является переменной дифференцирования, он просто игнорируется.

Опция nouns раскрывает вообще все несовершённые формы — и производные в том числе:

Img 82 110 3.png

Опция float преобразовывает все рациональные числа в конечную десятичную запись; опция numer включает опцию float и, кроме того, приводит к десятичному виду многие математические функции от числовых аргументов:

Img 82 110 4.png

Опция noeval блокирует сам этап вычисления как таковой; то есть её можно использовать для того, чтобы применить к выражению другие опции функции ev, не перевычисляя его. При этом опять-таки нужно понимать разницу между вычислением и упрощением:

Img 82 110 5.png

Таким образом, мы можем принудительно упростить выражение, не перевычисляя его.

Опция eval — напротив, проводит дополнительно ещё один процесс вычисления. Здесь стоит поговорить подробнее о накопительном эффекте вычисления, который я уже демонстрировал выше. Так как в Максиме значениями символов могут выступать самые разнообразные выражения, то в эти выражения тоже могут входить некоторые символы, которые тоже могут иметь свои значения; и такая цепочка «вложенных значений» может продолжаться сколь угодно глубоко. Один вызов функции ev (без опции eval) опускается по этой цепочке в глубину на один уровень:

Img 82 110 6.png

Напомню, что здесь ev(y), eval является сокращённой записью от ev(ev(y), eval), таким образом вычисление в этом выражении проводится трижды. Кроме того, хочу обратить ваше внимание на порядок назначения выражений символам; здесь существенно, что на момент задания каждого выражения входящий в него символ ещё не был определён — иначе в выражение автоматически подставлялся не сам символ, а его значение. Таким образом, если бы мы произвели эти же назначения в обратном порядке, то значением символа y стало бы xm+6 — безо всяких принудительных вычислений.

В продолжение разговора о накопительном эффекте и «цепочных» вычислениях придётся кстати переключатель infeval. Он заставляет ev перевычислять выражение до тех пор, пока оно не перестанет изменяться при последующих вычислениях. В частности, этот переключатель можно использовать и для того, чтобы разблокировать блокировку вычислений любой глубины вложения:

Img 82 111 1.png

В других ситуациях использовать этот переключатель следует с осторожностью: не забывайте, что он может привести к зацикливанию.

О других константных опциях и переключателях функции ev можно узнать из ? ev и ? evflag, а мы наверняка ещё рассмотрим многие из них позже, когда они будут более актуальны в контексте повествования.

Кроме константных значений есть ещё несколько видов опций. Первый из них — это имена специальных функций, которые занимаются упрощением или преобразованием математических выражений. Будучи упомянута по имени в качестве опции, такая функция просто применяется к вычисляемому выражению. Например, выражение, fullratsimp - это то же самое, что и fullratsimp(ev(выражение)). Полный список таких функций вы можете найти в ? evfun.

Если в качестве опции ввести имя любой другой функции, не имеющей свойства evfun, то все несовершённые вхождения этой функции будут заменены совершёнными, то есть принудительно вычислены.


Также в качестве опции можно задать назначение символа или функции; все такие назначения действуют локально в пределах вычисляемого выражения, и все подстановки производятся параллельно:

Img 82 111 2.png

Опция подстановки символа допустима не только в виде оператора присвоения, но и в виде равенства; сделано это, в частности, для того, чтобы в качестве подстановок можно было использовать решения, найденные функцией solve:

Img 82 111 3.png

Вот и всё на сегодня. В следующий раз мы начнём с уже упомянутых вскользь функций по упрощению и преобразованию выражений.



Источник — «http://wiki.linuxformat.ru/wiki/index.php?title=LXF82:Maxima&oldid=6334»
Персональные инструменты
купить
подписаться
Яндекс.Метрика