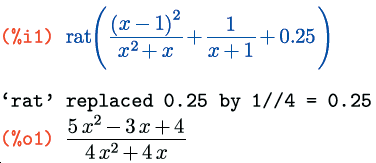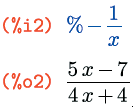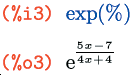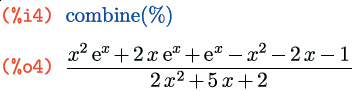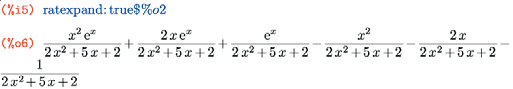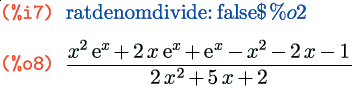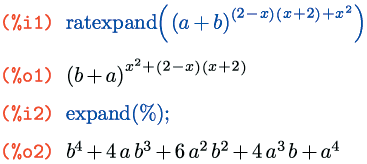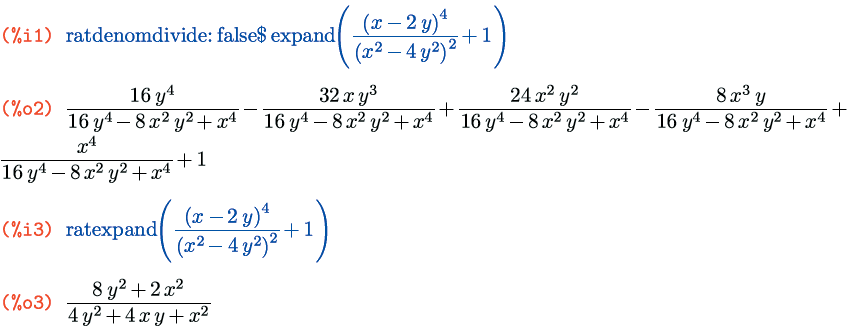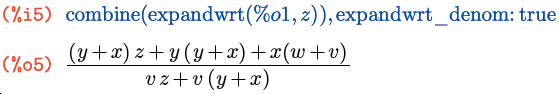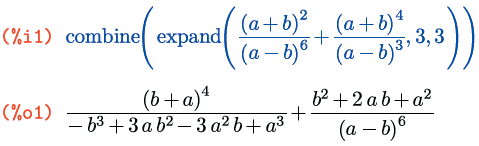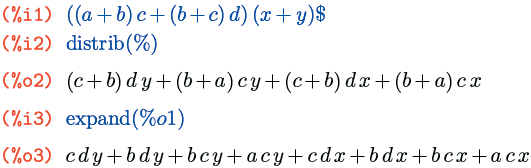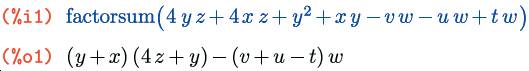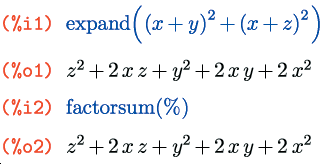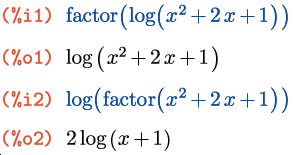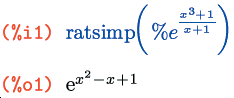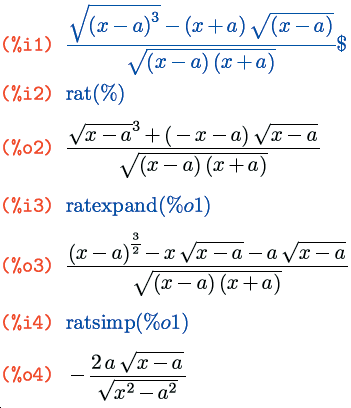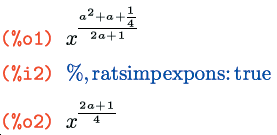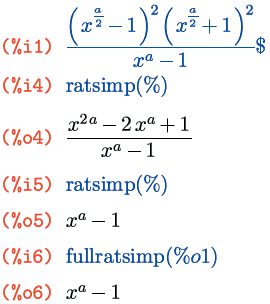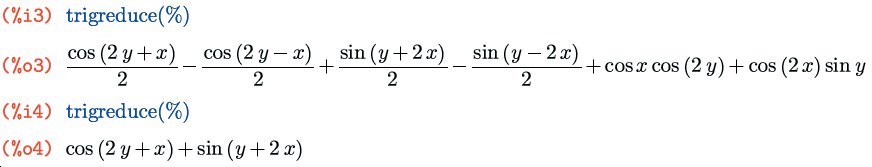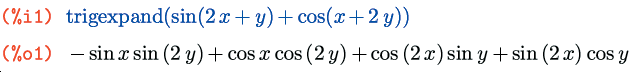LXF83:Maxima
(Новая: == Maxima: укротитель выражений == '' '''ЧАСТЬ 3''' Сегодня '''Тихон Тарнавский''' расскажет вам о возможностях Max...) |
Pvm (обсуждение | вклад) (Категории) |
||
| (не показаны 10 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| + | {{Цикл/Maxima}} | ||
| + | |||
== Maxima: укротитель выражений == | == Maxima: укротитель выражений == | ||
| − | '' ''' | + | '' '''Часть 3''' Сегодня '''Тихон Тарнавский''' расскажет вам о возможностях Maxima по <strike>укрощению</strike> упрощению выражений, содержащих рациональные, иррациональные и тригонометрические функции.'' |
В этот раз я расскажу о штатных возможностях Maxima по упрощению и прочим преобразованиям выражений. В частности, речь пойдет об автоматическом раскрытии скобок и вынесении за скобки; об упрощении как арифметических действий над некоторыми элементами, так и выражений с участием степенных, показательных и логарифмических функций; а также об обработке тригонометрических выражений. Все эти функции призваны облегчать читаемость математических формул и повышать простоту их восприятия, а посему стоит уделить этому уроку достаточно внимания: при верном использовании данные манипуляции позволят сэкономить в процессе работы значительное количество времени. | В этот раз я расскажу о штатных возможностях Maxima по упрощению и прочим преобразованиям выражений. В частности, речь пойдет об автоматическом раскрытии скобок и вынесении за скобки; об упрощении как арифметических действий над некоторыми элементами, так и выражений с участием степенных, показательных и логарифмических функций; а также об обработке тригонометрических выражений. Все эти функции призваны облегчать читаемость математических формул и повышать простоту их восприятия, а посему стоит уделить этому уроку достаточно внимания: при верном использовании данные манипуляции позволят сэкономить в процессе работы значительное количество времени. | ||
=== Выражаясь рационально... === | === Выражаясь рационально... === | ||
| − | Существенная часть интересующих нас сегодня функций | + | Существенная часть интересующих нас сегодня функций предназначена для преобразования рациональных выражений. Напомню, рациональным называется выражение, состоящее только из арифметических операторов и возведения в натуральную степень; естественно, элементы такого выражения могут содержать и неарифметические и нестепенные функции – тогда такие элементы с точки зрения рационального выражения считаются атомарными, т.е. неделимыми и непреобразуемыми. |
| − | + | ||
| − | + | Функции, работающие с рациональными выражениями, описаны в разделе документации «Polynomials»; потому как рациональные функции с математической точки зрения рассматриваются как расширение многочленов (полиномов) – примерно так же, как рациональные числа считаются расширением целых (многочлены, кстати, тоже иногда называют целыми функциями; хотя общий математический смысл этого термина несколько шире). | |
| − | операторов и возведения в натуральную степень; естественно, элементы | + | |
| − | такого выражения могут содержать и неарифметические и нестепенные | + | Имена всех функций Maxima по обработке рациональных выражений содержат буквосочетание rat, но не от слова «крыса», а от слова «rational». И начнем мы знакомство с ними с функции, которая так и называется: rat(выражение). Эта функция преобразовывает рациональное выражение к так называемой канонической форме (Canonical Rational Expression, CRE). То есть раскрывает все скобки, затем приводит все к общему знаменателю, суммирует и сокращает; кроме того, приводит все числа в конечной десятичной записи к рациональным. |
| − | функции – тогда такие элементы с точки зрения рационального | + | |
| − | + | [[Изображение:Img_83_86_1.png]] | |
| − | Функции, работающие с рациональными выражениями, описаны | + | |
| − | в разделе документации «Polynomials»; потому как рациональные | + | Тут надо заметить, что атомарные элементы, т.е. символы и числа, в канонической форме рационального выражения в Maxima имеют другое внутреннее представление. При работе в интерфейсах Maxima и xMaxima об этом напоминает приписка /R/ после имени ячейки вывода (в wxMaxima и TeXmacs такая приписка отсутствует). При этом внешне, на видимом пользователю уровне, каноническая форма ничем, кроме этого обозначения, от общей не отличается. Но один достаточно интересный момент здесь есть: если каноническая форма рационального выражения используется в других рациональных выражениях, то последние также автоматически приводятся к канонической форме: |
| − | функции с математической точки зрения рассматриваются как | + | |
| − | + | [[Изображение:Img_83_86_2.png]] | |
| − | числа считаются расширением целых (многочлены, кстати, тоже иногда | + | |
| − | называют целыми функциями; хотя общий математический смысл этого | + | Это может быть достаточно удобно, если вам нужно пошагово проделать большое количество рациональных преобразований: вы можете, один раз вызвав rat(), ссылаться на предыдущие ячейки и благодаря этому далее автоматически видеть на каждом шаге итоговое выражение в канонической, а значит, достаточно компактной и удобной к восприятию, форме. Если на каком-то этапе такое поведение станет вам мешать, вы можете вернуть выражение из канонической к общей форме с помощью функции ratdisrep(выражение). Кроме того, каноническая форма автоматически «отменяется» и в случае любых преобразований, не являющихся рациональными: |
| − | термина несколько шире). | + | |
| − | Имена всех функций Maxima по обработке рациональных | + | [[Изображение:Img_83_86_3.png]] |
| − | + | ||
| − | «rational». И начнем мы знакомство с ними с функции, которая так и | + | Здесь, хотя %o2 было выражением в канонической форме, %o3 – уже выражение общего вида, так как оно не является рациональным. |
| − | называется: rat(выражение). Эта функция преобразовывает | + | |
| − | + | Скажем пару слов о приведении конечной десятичной записи чисел к рациональной. Конечная десятичная запись считается по определению приблизительной, что и понятно, т.к. при вычислениях самой Maxima такая запись может возникнуть исключительно при применении приближенных методов либо при ручном указании о переводе числа в десятичную запись из математической, в результате чего результат тоже, вероятнее всего, окажется приблизительным. Эта приблизительность учитывается и при переводе в рациональные числа, а ее уровень, то есть мера, на которую рациональное число при переводе может отклониться от конечной десятичной записи, регулируется переменной ratepsilon, равной по умолчанию 2.0e-8, т.е. 0.00000002. Если такое положение вещей вас не устраивает, вы можете убедить Maxima оставлять десятичную запись чисел как есть, установив в true значение флага keepfloat (по умолчанию он равен false). | |
| − | Rational Expression, CRE). То есть раскрывает все скобки, затем приводит | + | |
| − | все к общему знаменателю, суммирует и сокращает; кроме того, | + | Следующая функция раскрывает скобки в рациональном выражении и называется ratexpand() (одно из значений слова expand и есть «раскрыть скобки»). Здесь также действует опция keepfloat. Кроме нее, есть еще одна опция – ratdenomdivide; по умолчанию она установлена в true, что приводит к тому, что каждая дробь, в которой числитель является суммой, распадается на сумму дробей с одинаковым знаменателем. Если же сбросить эту опцию в false, тогда все дроби с одинаковым знаменателем будут, напротив, объединены в одну дробь с числителем в виде суммы числителей изначальных дробей. То есть внешне результат будет в этом случае выглядеть почти так же, как и у функции rat(); к тому же единственная видимая пользователю разница проявляется только в рациональных выражениях от нескольких переменных (или различных иррациональных выражений). Заключается эта разница в том, что после ratexpand() и в числителе, и в знаменателе дроби все скобки будут раскрыты, в случае же rat() слагаемые, где присутствуют, скажем, две переменных, будут сгруппированы, и одна из них будет вынесена за скобки (в документации такая форма записи называется «рекурсивной» (recursive): |
| − | + | ||
| − | Тут надо заметить, что атомарные элементы, т.е. символы и | + | [[Изображение:Img_83_87_1.png]] |
| − | + | ||
| − | другое внутреннее представление. При работе в интерфейсах Maxima и | + | Кроме того, разница, конечно, заключается и во внутреннем представлении: с точки зрения программы, после ratexpand() выражение будет по-прежнему общего вида. Соответственно и все результаты дальнейших рациональных действий с выражением не будут автоматически «канонизироваться». Я специально обращаю ваше внимание на схожесть между результатами этих двух различных функций, поскольку в документации эта схожесть никак не обозначена: в описании обеих функций и примерах к ним нет вообще никаких ссылок друг на друга. |
| − | xMaxima об этом напоминает приписка /R/ после имени ячейки вывода | + | |
| − | (в wxMaxima и TeXmacs такая приписка отсутствует). При этом внешне, | + | Помимо флага ratdenomdivide, есть также функция, собирающая воедино дроби с одинаковыми знаменателями; зовут ее combine(): |
| − | на видимом пользователю уровне, каноническая форма ничем, кроме | + | |
| − | + | [[Изображение:Img_83_87_2.png]] | |
| − | этого обозначения, от общей не отличается. Но один достаточно | + | |
| − | + | В дополнение к функции ratexpand() есть также флаг ratexpand, который по умолчанию равен false, а будучи установлен в true, приводит к тому, что все рациональные выражения в канонической форме отображаются и преобразовываются к общему виду сразу же с раскрытыми скобками: | |
| − | выражения используется в других рациональных выражениях, то | + | |
| − | + | [[Изображение:Img_83_87_3.png]] | |
| − | Это может быть достаточно удобно, если вам нужно пошагово | + | |
| − | + | Обратите внимание, что при применении этого флага выражение сохраняет каноническую форму. | |
| − | один раз вызвав rat(), ссылаться на предыдущие ячейки и благодаря | + | |
| − | этому далее автоматически видеть на каждом шаге итоговое | + | Действует в этом случае и флаг ratdenomdivide (напомню, что в строке %i1 этот флаг был установлен локально, используя сокращенную запись функции ev()): |
| − | + | ||
| − | + | [[Изображение:Img_83_87_4.png]] | |
| − | мешать, вы можете вернуть выражение из канонической к общей форме | + | |
| − | с помощью функции ratdisrep(выражение). Кроме того, каноническая | + | Иными словами, флаг ratexpand по своему действию аналогичен одноименной функции, но действует он на все без исключения канонические рациональные выражения и при этом оставляет их в канонической внутренней записи и изменяет только внешнее отображение этой записи, сохраняя при этом и дальнейшую автоматическую «канонизацию». |
| − | форма автоматически «отменяется» и в случае любых преобразований, | + | |
| − | не являющихся рациональными: | + | |
| − | Здесь, хотя %o2 было выражением в канонической форме, %o3 – | + | |
| − | уже выражение общего вида, так как оно не является рациональным. | + | |
| − | Скажем пару слов о приведении конечной десятичной записи чисел | + | |
| − | к рациональной. Конечная десятичная запись считается по | + | |
| − | + | ||
| − | Maxima такая запись может возникнуть исключительно при применении | + | |
| − | приближенных методов либо при ручном указании о переводе числа в | + | |
| − | десятичную запись из математической, в результате чего результат тоже, | + | |
| − | вероятнее всего, окажется приблизительным. Эта приблизительность | + | |
| − | учитывается и при переводе в рациональные числа, а ее уровень, то есть | + | |
| − | мера, на которую рациональное число при переводе может отклониться | + | |
| − | от конечной десятичной записи, регулируется переменной ratepsilon, | + | |
| − | равной по умолчанию 2.0e-8, т.е. 0.00000002. Если такое положение | + | |
| − | вещей вас не устраивает, вы можете убедить Maxima оставлять | + | |
| − | + | ||
| − | (по умолчанию он равен false). | + | |
| − | Следующая функция раскрывает скобки в рациональном | + | |
| − | + | ||
| − | «раскрыть скобки»). Здесь также действует опция keepfloat. Кроме нее, | + | |
| − | есть еще одна опция – ratdenomdivide; по умолчанию она | + | |
| − | + | ||
| − | является суммой, распадается на сумму дробей с одинаковым | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | результат будет в этом случае выглядеть почти так же, как и у функции | + | |
| − | rat(); к тому же единственная видимая пользователю разница | + | |
| − | + | ||
| − | (или различных иррациональных выражений). Заключается эта разница | + | |
| − | в том, что после ratexpand() и в числителе, и в знаменателе дроби все | + | |
| − | скобки будут раскрыты, в случае же rat() слагаемые, где присутствуют, | + | |
| − | скажем, две переменных, будут сгруппированы, и одна из них будет | + | |
| − | вынесена за скобки (в документации такая форма записи называется | + | |
| − | «рекурсивной» (recursive): | + | |
| − | Кроме того, разница, конечно, заключается и во внутреннем | + | |
| − | + | ||
| − | будет по-прежнему общего вида. Соответственно и все результаты | + | |
| − | дальнейших рациональных действий с выражением не будут | + | |
| − | + | ||
| − | схожесть между результатами этих двух различных функций, поскольку | + | |
| − | в документации эта схожесть никак не обозначена: в описании обеих | + | |
| − | функций и примерах к ним нет вообще никаких ссылок друг на друга. | + | |
| − | Помимо флага ratdenomdivide, есть также функция, собирающая | + | |
| − | воедино дроби с одинаковыми знаменателями; зовут ее combine(): | + | |
| − | В дополнение к функции ratexpand() есть также флаг ratexpand, | + | |
| − | который по умолчанию равен false, а будучи установлен в true, | + | |
| − | + | ||
| − | отображаются и преобразовываются к общему виду сразу же с | + | |
| − | + | ||
| − | Обратите внимание, что при применении этого флага выражение | + | |
| − | сохраняет каноническую форму. | + | |
| − | Действует в этом случае и флаг ratdenomdivide (напомню, что в | + | |
| − | строке %i1 этот флаг был установлен локально, используя | + | |
| − | + | ||
| − | Иными словами, флаг ratexpand по своему действию | + | |
| − | + | ||
| − | канонические рациональные выражения и при этом оставляет их в | + | |
| − | канонической внутренней записи и изменяет только внешнее | + | |
| − | + | ||
| − | «канонизацию». | + | |
=== ...и не только рационально. === | === ...и не только рационально. === | ||
| − | Помимо ratexpand() есть также и функция «просто» expand(). | + | Помимо ratexpand() есть также и функция «просто» expand(). Различий между ними несколько, наиболее принципиальные таковы. Во-первых, ratexpand() раскрывает только рациональное выражение «верхнего уровня», все же подвыражения, не являющиеся рациональными, обрабатываются как атомарные, то есть внутрь них она не залезает; expand() же раскрывает скобки на всех уровнях вложенности: |
| − | Различий между ними несколько, наиболее принципиальные таковы. Во- | + | |
| − | первых, ratexpand() раскрывает только рациональное выражение | + | |
| − | + | ||
| − | обрабатываются как атомарные, то есть внутрь них она не залезает; | + | |
| − | expand() же раскрывает скобки на всех уровнях вложенности | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | (На предупреждение, возникающее при первом вызове функций | + | [[Изображение:Img_83_87_5.png]] |
| − | expandwrt*(), можете не обращать внимания – на функционале, о | + | |
| − | + | Во-вторых, ratexpand() приводит дроби-слагаемые к общему знаменателю, а expand() этого не делает; в-третьих, на функцию expand не действует переключатель ratdenomdivide: | |
| − | Если в выражении встречаются дроби, то по умолчанию эта | + | |
| − | + | [[Изображение:Img_83_87_6.png]] | |
| − | в покое. Изменить это поведение можно переключателем | + | |
| − | + | И в-четвертых, expand() не преобразовывает к рациональным числам конечную десятичную запись – опять-таки, вне зависимости от флага keepfloat. | |
| − | И, наконец, последняя функция из этого семейства – | + | |
| − | + | Функция expand(), в отличие от своего рационального сородича, имеет несколько вариаций – в виде отдельных функций с похожими названиями, которые раскрывают скобки несколько по-разному. Первую мы уже рассмотрели. Вторая называется expandwrt(выражение, x, y, ..., v), где wrt расшифровывается как «with respect to...», то есть «относительно...». Она раскрывает скобки не везде, а только относительно тех символов, которые заданы в списке аргументов после выражения. Другими словами, только там, где из скобок можно вынести хотя бы один из перечисленных символов: | |
| − | + | ||
| − | из сомножителей: | + | [[Изображение:Img_83_87_7.png]] |
| − | Раскрытием возведения в целую степень можно управлять как в | + | |
| − | контексте функции expand(), так и отдельно. В первом случае | + | (На предупреждение, возникающее при первом вызове функций expandwrt*(), можете не обращать внимания – на функционале, о котором идет речь, оно никоим образом не отражается.) |
| − | + | ||
| − | + | Если в выражении встречаются дроби, то по умолчанию эта функция раскрывает скобки только в их числителях, оставляя знаменатели в покое. Изменить это поведение можно переключателем expandwrt_denom, установив его в true (по умолчанию он равен false): | |
| − | которые будут раскрываться этой функцией. По умолчанию оба | + | |
| − | + | [[Изображение:Img_83_88_1.png]] | |
| − | и в контексте одного конкретного вызова функции expand() – в таком | + | |
| − | случае это делается с помощью дополнительных аргументов, | + | И, наконец, последняя функция из этого семейства – expandwrt_factored(выражение, x, y, ..., v) – раскрывает скобки лишь в тех слагаемых, где упомянутые символы встречаются не в одном, а в каждом из сомножителей: |
| − | + | ||
| − | В противовес maxposex и maxnegex можно задать максимальные | + | [[Изображение:Img_83_88_2.png]] |
| − | положительную и отрицательную степени, которые будут раскрываться | + | |
| − | автоматически, без вызова функций группы expand. За это отвечают | + | Раскрытием возведения в целую степень можно управлять как в контексте функции expand(), так и отдельно. В первом случае применяются переменные maxposex и maxnegex, определяющие соответственно максимальные положительный и отрицательный показатель степени, которые будут раскрываться этой функцией. По умолчанию оба параметра равны 1000. Переназначить их можно не только глобально, но и в контексте одного конкретного вызова функции expand() – в таком случае это делается с помощью дополнительных аргументов, задаваемых после выражения: |
| − | переменные expop и expon, и по умолчанию они равны нулю, то есть | + | |
| − | автоматически степени не раскрываются вообще. | + | [[Изображение:Img_83_88_3.png]] |
| − | Кроме самостоятельной функции expand(), существуют также | + | |
| − | + | В противовес maxposex и maxnegex можно задать максимальные положительную и отрицательную степени, которые будут раскрываться автоматически, без вызова функций группы expand. За это отвечают переменные expop и expon, и по умолчанию они равны нулю, то есть автоматически степени не раскрываются вообще. | |
| − | равносильна expand(ev(выражение)), а выражение, expand(p, n) – | + | |
| − | expand(ev(выражение, p, n)). | + | Кроме самостоятельной функции expand(), существуют также флаги expand и expand(p, n) у функции ev(). Запись выражение, expand равносильна expand(ev(выражение)), а выражение, expand(p, n) – expand(ev(выражение, p, n)). |
| − | Возможности управлять раскрытием скобок на этом не | + | |
| − | + | Возможности управлять раскрытием скобок на этом не заканчиваются. Еще одна функция – distrib() – представляет как бы облегченный вариант expand(). Она действует аналогично expand(), но только на один уровень в глубину: | |
| − | вариант expand(). Она действует аналогично expand(), но только на | + | |
| − | один уровень в глубину: | + | [[Изображение:Img_83_88_4.png]] |
| − | В противоположность функциям *expand*(), раскрывающим | + | |
| − | + | В противоположность функциям *expand*(), раскрывающим скобки, можно также и разложить выражение на множители, то есть максимально повыносить все за скобки. Делается это с помощью функции factor(): | |
| − | + | ||
| − | factor(): | + | [[Изображение:Img_83_88_5.png]] |
| − | Если функции factor() передать целое число, она разложит его на | + | |
| − | простые множители; если же передать рациональное число – на | + | Если функции factor() передать целое число, она разложит его на простые множители; если же передать рациональное число – на множители будут разложены его числитель и знаменатель: |
| − | + | ||
| − | Если многочлен не может быть представлен в виде произведения | + | [[Изображение:Img_83_88_6.png]] |
| − | нескольких сомножителей, его можно попытаться преобразовать в | + | |
| − | + | Если многочлен не может быть представлен в виде произведения нескольких сомножителей, его можно попытаться преобразовать в сумму таких произведений с помощью функции factorsum(): | |
| − | Функция factorsum() умеет раскладывать на множители только | + | |
| − | независимые слагаемые, то есть такие, которые не содержат | + | [[Изображение:Img_83_88_7.png]] |
| − | + | ||
| − | двух разных местах один и тот же символ, то так как коэффициенты при | + | Функция factorsum() умеет раскладывать на множители только независимые слагаемые, то есть такие, которые не содержат одинаковых переменных. Если мы раскроем скобки в выражении, содержащем в двух разных местах один и тот же символ, то так как коэффициенты при этом символе после раскрытия сгруппируются, factorsum() не сможет понять, каким именно образом разгруппировать их обратно: |
| − | этом символе после раскрытия сгруппируются, factorsum() не сможет | + | |
| − | понять, каким именно образом разгруппировать их обратно: | + | [[Изображение:Img_83_88_8.png]] |
| − | Нужно заметить, что функции factor() и factorsum(), хотя и не | + | |
| − | имеют в имени приставки rat, все же ведут себя в смысле разбора | + | Нужно заметить, что функции factor() и factorsum(), хотя и не имеют в имени приставки rat, все же ведут себя в смысле разбора передаваемых им выражений не как expand() и сопутствующие, а как ratexpend(); то есть на любой не-рациональной функции останавливаются и внутрь не идут: |
| − | передаваемых им выражений не как expand() и сопутствующие, а как | + | |
| − | ratexpend(); то есть на любой не-рациональной функции | + | [[Изображение:Img_83_88_9.png]] |
| − | + | ||
| − | Впрочем, об этом можно догадаться из документации, так как | + | Впрочем, об этом можно догадаться из документации, так как функции factor* описаны не в разделе Simplification, куда относятся expand*, а, так же, как и rat*, в разделе Polynomials. |
| − | функции factor* описаны не в разделе Simplification, куда относятся | + | |
| − | expand*, а, так же, как и rat*, в разделе Polynomials. | + | Выносить за скобки, а также раскрывать эти скобки можно не только специальной функцией, но и дополнительным флагом ко все той же канонической форме рациональных выражений. Флаг этот зовут ratfac, и по умолчанию он равен false, то есть вынесение за скобки не происходит. Если же его установить в true, то в каждом рациональном выражении, приведенном к канонической форме, все будет максимально вынесено за скобки, но без вызова функции factor(); например, в примере ниже не произошло обратного свертывания (x+1)<sup>2</sup>, хотя, будучи применен к первоначальному выражению, флаг ratfac сохранил и этот множитель нераскрытым (также можете сравнить этот пример с аналогичным примером к функциям ratexpand() и rat()): |
| − | Выносить за скобки, а также раскрывать эти скобки можно не | + | |
| − | + | [[Изображение:Img_83_89_1.png]] | |
| − | же канонической форме рациональных выражений. Флаг этот зовут | + | |
| − | ratfac, и по умолчанию он равен false, то есть вынесение за скобки не | + | |
| − | происходит. Если же его установить в true, то в каждом рациональном | + | |
| − | выражении, приведенном к канонической форме, все будет | + | |
| − | + | ||
| − | + | ||
| − | хотя, будучи применен к первоначальному выражению, флаг ratfac | + | |
| − | сохранил и этот множитель нераскрытым (также можете сравнить этот | + | |
| − | пример с аналогичным примером к функциям ratexpand() и rat()): | + | |
=== Проще простого === | === Проще простого === | ||
| − | Итак, о преобразованиях выражений мы уже поговорили | + | Итак, о преобразованиях выражений мы уже поговорили достаточно – теперь перейдем к их упрощению. Об элементарных упрощениях мы уже говорили в предыдущий раз: они могут производиться автоматически, на что влияет установленный флаг simp; и по умолчанию именно так и происходит. |
| − | + | ||
| − | мы уже говорили в предыдущий раз: они могут производиться | + | Здесь тоже все начинается с рациональных выражений, которыми занимается функция ratsimp(выражение). Она упрощает выражение за счет рациональных преобразований, но, в отличие от остальных функций по обработке рациональных выражений, работает в том числе и «вглубь», то есть иррациональные части выражения не рассматриваются как атомарные, а упрощаются, в том числе, и все рациональные элементы внутри них: |
| − | + | ||
| − | именно так и происходит. | + | [[Изображение:Img_83_89_2.png]] |
| − | Здесь тоже все начинается с рациональных выражений, которыми | + | |
| − | занимается функция ratsimp(выражение). Она упрощает выражение | + | На ratsimp() действуют те же флаги, что и на rat(): и ratexpand, и keepfloat, и ratfac. Но отличается она от rat() или ratexpand() не только умением работать «в глубину», но и некоторыми дополнительными рациональными преобразованиями, которые не поддерживаются этими двумя функциями: |
| − | за счет рациональных преобразований, но, в отличие от остальных | + | |
| − | функций по обработке рациональных выражений, работает в том числе | + | [[Изображение:Img_83_89_3.png]] |
| − | и «вглубь», то есть иррациональные части выражения не | + | |
| − | + | Кроме функции ratsimp(), есть еще и дополнительный переключатель – ratsimpexpons. По умолчанию он установлен в false; если же назначить ему значение true – это приведет к автоматическому упрощению показателей степени: | |
| − | элементы внутри них: | + | |
| − | На ratsimp() действуют те же флаги, что и на rat(): и ratexpand, и | + | [[Изображение:Img_83_89_4.png]] |
| − | keepfloat, и ratfac. Но отличается она от rat() или ratexpand() не | + | |
| − | + | Функция ratsimp() – это уже достаточно мощный, и в то же время весьма быстрый, механизм упрощения; но, конечно, не достаточный: ведь те действия, которые можно упростить в разнообразных математических выражениях, не ограничиваются рациональными. Поэтому все же основной плюс этой функции – это скорость. А для более серьезных упрощений существует расширенный вариант – fullratsimp(выражение). Эта функция последовательно применяет к переданному выражению функцию ratsimp(), а также некоторые нерациональные преобразования – и повторяет эти действия в цикле до тех пор, пока выражение не перестанет в процессе них изменяться. За счет этого функция работает несколько медленнее, чем ratsimp(), зато дает более надежный результат – к некоторым выражениям, которые она может упростить с ходу, ratsimp() пришлось бы применять несколько раз, а иногда та и вообще не справилась бы с задачей. | |
| − | рациональными преобразованиями, которые не поддерживаются этими | + | |
| − | двумя функциями: | + | [[Изображение:Img_83_89_5.png]] |
| − | Кроме функции ratsimp(), есть еще и дополнительный | + | |
| − | + | И третья основная функция упрощения выражений – уже никак с предыдущими двумя не соотносящаяся – radcan(выражение). Если ratsimp() и fullratsimp() ориентированы на упрощение рациональных действий, то radcan() занимается упрощением логарифмических, экспоненциальных функций и степенных с нецелыми рациональными показателями, то есть корней (радикалов). Например, выражение из второго примера в этом разделе radcan() сможет упростить сильнее, чем ratsimp()/fullratsimp(): | |
| − | назначить ему значение true – это приведет к автоматическому | + | |
| − | + | [[Изображение:Img_83_89_6.png]] | |
| − | Функция ratsimp() – это уже достаточно мощный, и в то же | + | |
| − | время весьма быстрый, механизм упрощения; но, конечно, не | + | [[Изображение:Img_83_90_1.png]] |
| − | + | ||
| − | + | В некоторых случаях наилучшего результата можно добиться, комбинируя radcan() с ratsimp() или fullratsimp(). | |
| − | + | ||
| − | для более серьезных упрощений существует расширенный вариант – | + | С функцией radcan() смежны по действию еще два управляющих ключа. Один из них называется %e_to_numlog. Влияет он не на саму функцию, а на автоматическое упрощение. Если выставить его в true, то выражения вида e<sup>(r*log(выражение))</sup>, где r – рациональное число, будут автоматически раскрываться в выражениеr. Функция radcan() делает такие преобразования независимо от значения ключа. Второй ключ – radexpand (от radical, не путать с ratexpand) – влияет на упрощение квадратного корня из четной степени какого-либо выражения. Он, в отличие от большинства переключателей, имеет не два, а три значения: при значении all, sqrt(x<sup>2</sup>) будет раскрываться в x – как для действительных, так и для комплексных чисел; при значении true (по умолчанию), sqrt(x<sup>2</sup>) для действительных чисел превращается в |x|, а для комплексных не преобразуется; а при значении false, sqrt(x<sup>2</sup>) не будет упрощаться вообще. |
| − | fullratsimp(выражение). Эта функция последовательно применяет | + | |
| − | к переданному выражению функцию ratsimp(), а также некоторые | + | Следующие две функции и один флаг относятся к упрощению факториалов. Функция factcomb(выражение) проводит упрощения вида n!*(n+1) = (n+1)! и тому подобные. Функция minfactorial, напротив, сокращает факториалы, то есть действует по принципу n!/(n–1)! = n. И флаг sumsplitfact, который изначально установлен в true, находясь в состоянии false, приводит к тому, что после того, как отработает factcomb, minfactorial вызывается автоматически. |
| − | + | ||
| − | тех пор, пока выражение не перестанет в процессе них изменяться. За | + | |
| − | счет этого функция работает несколько медленнее, чем ratsimp(), зато | + | |
| − | дает более надежный результат – к некоторым выражениям, которые | + | |
| − | она может упростить с ходу, ratsimp() пришлось бы применять | + | |
| − | + | ||
| − | И третья основная функция упрощения выражений – уже никак с | + | |
| − | предыдущими двумя не соотносящаяся – radcan(выражение). Если | + | |
| − | ratsimp() и fullratsimp() ориентированы на упрощение | + | |
| − | + | ||
| − | экспоненциальных функций и степенных с нецелыми рациональными | + | |
| − | показателями, то есть корней (радикалов). Например, выражение из | + | |
| − | второго примера в этом разделе radcan() сможет упростить сильнее, | + | |
| − | чем ratsimp()/fullratsimp(): | + | |
| − | В некоторых случаях наилучшего результата можно добиться, | + | |
| − | + | ||
| − | С функцией radcan() смежны по действию еще два | + | |
| − | + | ||
| − | саму функцию, а на автоматическое упрощение. Если выставить его в | + | |
| − | true, то выражения вида e(r*log(выражение)), где r – рациональное число, | + | |
| − | будут автоматически раскрываться в выражениеr. Функция radcan() | + | |
| − | делает такие преобразования независимо от значения ключа. Второй | + | |
| − | ключ – radexpand (от radical, не путать с ratexpand) – влияет на | + | |
| − | упрощение квадратного корня из четной степени какого-либо | + | |
| − | + | ||
| − | значения: при значении all, sqrt( | + | |
| − | действительных, так и для комплексных чисел; при значении true (по | + | |
| − | умолчанию), sqrt( | + | |
| − | для комплексных не преобразуется; а при значении false, sqrt( | + | |
| − | будет упрощаться вообще. | + | |
| − | Следующие две функции и один флаг относятся к упрощению | + | |
| − | + | ||
| − | n!*(n+1) = (n+1)! и тому подобные. Функция minfactorial, напротив, | + | |
| − | сокращает факториалы, то есть действует по принципу n!/(n–1)! = n. | + | |
| − | И флаг sumsplitfact, который изначально установлен в true, | + | |
| − | + | ||
| − | factcomb, minfactorial вызывается автоматически. | + | |
=== Вот под таким углом... === | === Вот под таким углом... === | ||
| − | И напоследок поговорим о функциях для преобразования | + | И напоследок поговорим о функциях для преобразования тригонометрических формул. Здесь так же, как и у рациональных функций, присутствует общая для всех приставка – trig; расшифровывать ее, думаю, особой нужды нет. Начнем по традиции с функции trigexpand(выражение). Она, как нетрудно догадаться, раскрывает скобки в тригонометрических выражениях: |
| − | + | ||
| − | + | [[Изображение:Img_83_90_2.png]] | |
| − | + | ||
| − | trigexpand(выражение). Она, как нетрудно догадаться, раскрывает | + | Здесь, как обычно, есть несколько управляющих флагов, первый из которых опять же является тезкой самой функции. Он приводит к повторному раскрытию всех синусов-косинусов, то есть фактически равнозначен повторному вызову самой функции: |
| − | скобки в тригонометрических выражениях: | + | |
| − | Здесь, как обычно, есть несколько управляющих флагов, первый | + | [[Изображение:Img_83_90_2.png]] |
| − | из которых опять же является тезкой самой функции. Он приводит к | + | |
| − | повторному раскрытию всех синусов-косинусов, то есть фактически | + | Второй флаг – halfangles – управляет раскрытием формул половинных углов. Оба эти флага по умолчанию сброшены. А следующие два флага – trigexpandplus и trigexpandtimes – отвечают соответственно за применение формул сумм углов и кратных углов. То есть в примере выше сначала сработал флаг trigexpandplus, а затем – trigexpandtimes. Эти флаги по умолчанию установлены, что и видно из примера. |
| − | равнозначен повторному вызову самой функции: | + | |
| − | Второй флаг – halfangles – управляет раскрытием формул | + | Кроме всего уже упомянутого, есть еще флаги trigsign и triginverses. Первый принимает традиционные два значения (по умолчанию – true) и регулирует вынос знака за пределы тригонометрической функции, то есть, к примеру, sin(–x) упростится до –sin(x), а cos(–x) – до cos(x). Флаг triginverses – трехзначный, и умолчательное его значение равно all. Он отвечает за обработку сочетаний вида sin(asin(x)) или atan(tan(x)). Значение all позволяет раскрывать эти сочетания в обоих направлениях (напомню, что при этом часть корней будет теряться); значение true оставляет разрешенным раскрытие только вида sin(asin(x)), то есть блокирует вариант с потерями периодических значений; а случай false запрещает оба направления преобразований. |
| − | + | ||
| − | два флага – trigexpandplus и trigexpandtimes – отвечают | + | Функция, обратная trigexpand(), называется trigreduce(выражение) – здесь, в полном соответствии со значением слова reduce, действуют формулы понижения степени. Например, применив дважды эту функцию к результату предыдущего примера, мы получим его в исходном виде (см. рис. наверху страницы). |
| − | + | ||
| − | в примере выше сначала сработал флаг trigexpandplus, а затем – | + | Эту функцию можно вызвать с более полным списком аргументов: trigreduce(выражение, переменная) – тогда формулы понижения степени будут применяться только по отношению к заданной переменной (переменная может быть, как и почти везде, не только отдельным символом, но и выражением). |
| − | trigexpandtimes. Эти флаги по умолчанию установлены, что и видно | + | |
| − | из примера. | + | Третья функция занимается уже упрощением, и зовут ее, соответственно, trigsimp(выражение). Она старается упростить любое тригонометрическое выражение, используя известные формулы, такие как sin<sup>2</sup>(x)+cos<sup>2</sup>(x)=1 и тому подобные. Для наилучшего результата ее можно комбинировать с trigreduce(), ratsimp()/fullratsimp() и radcan(). |
| − | Кроме всего уже упомянутого, есть еще флаги trigsign и triginverses. | + | |
| − | Первый принимает традиционные два значения (по умолчанию – true) | + | Этим возможности Maxima по преобразованию и упрощению разнообразных выражений еще не совсем исчерпаны, но основные из них мы рассмотрели в полной мере. В следующий раз поговорим немного о применении некоторых встроенных функций, о работе с векторами, матрицами и множествами и, возможно, о работе с логикой, с уравнениями и неравенствами, а также их системами. |
| − | и регулирует вынос знака за пределы тригонометрической функции, то | + | |
| − | есть, к примеру, sin(–x) упростится до –sin(x), а cos(–x) – до cos(x). | + | [[Категория:Математические пакеты]] |
| − | Флаг triginverses – трехзначный, и умолчательное его значение | + | [[Категория:Maxima]] |
| − | равно all. Он отвечает за обработку сочетаний вида sin(asin(x)) или | + | [[Категория:Учебники]] |
| − | atan(tan(x)). Значение all позволяет раскрывать эти сочетания в обоих | + | |
| − | направлениях (напомню, что при этом часть корней будет теряться); | + | |
| − | + | ||
| − | то есть блокирует вариант с потерями периодических значений; а случай | + | |
| − | false запрещает оба направления преобразований. | + | |
| − | Функция, обратная trigexpand(), называется trigreduce( | + | |
| − | + | ||
| − | + | ||
| − | функцию к результату предыдущего примера, мы получим его в | + | |
| − | + | ||
| − | Эту функцию можно вызвать с более полным списком аргументов: | + | |
| − | trigreduce(выражение, переменная) – тогда формулы понижения | + | |
| − | степени будут применяться только по отношению к заданной | + | |
| − | + | ||
| − | символом, но и выражением). | + | |
| − | Третья функция занимается уже упрощением, и зовут ее, | + | |
| − | + | ||
| − | + | ||
| − | как | + | |
| − | ее можно комбинировать с trigreduce(), ratsimp()/fullratsimp() и | + | |
| − | radcan(). | + | |
| − | Этим возможности Maxima по преобразованию и упрощению | + | |
| − | + | ||
| − | мы рассмотрели в полной мере. В следующий раз поговорим немного о | + | |
| − | применении некоторых встроенных функций, о работе с векторами, | + | |
| − | + | ||
| − | и неравенствами, а также их системами. | + | |
Текущая версия на 19:24, 22 октября 2008
|
|
|
- Метамодернизм в позднем творчестве В.Г. Сорокина
- ЛитРПГ - последняя отрыжка постмодерна
- "Ричард III и семиотика"
- 3D-визуализация обложки Ridero создаем обложку книги при работе над самиздатом.
- Архитектура метамодерна - говоря о современном искусстве, невозможно не поговорить об архитектуре. В данной статье будет отмечено несколько интересных принципов, характерных для построек "новой волны", столь притягательных и скандальных.
- Литература
- Метамодерн
- Рокер-Прометей против изначального зла в «Песне про советскую милицию» Вени Дркина, Автор: Нина Ищенко, к.ф.н, член Союза Писателей ЛНР - перепубликация из журнала "Топос".
- Как избавиться от комаров? Лучшие типы ловушек.
- Что делать если роблокс вылетает на windows
- Что делать, если ребенок смотрит порно?
- Почему собака прыгает на людей при встрече?
- Какое масло лить в Задний дифференциал (мост) Visco diff 38434AA050
- О чем может рассказать хвост вашей кошки?
- Верветки
- Отчетность бюджетных учреждений при закупках по Закону № 223-ФЗ
- Срок исковой давности как правильно рассчитать
- Дмитрий Патрушев минсельхоз будет ли преемником Путина
- Кто такой Владислав Поздняков? Что такое "Мужское Государство" и почему его признали экстремистским в России?
- Как правильно выбрать машинное масло в Димитровграде?
- Как стать богатым и знаменитым в России?
- Почему фильм "Пипец" (Kick-Ass) стал популярен по всему миру?
- Как стать мудрецом?
- Как правильно установить FreeBSD
- Как стать таким как Путин?
- Где лучше жить - в Димитровграде или в Ульяновске?
- Почему город Димитровград так называется?
- Что такое метамодерн?
- ВАЖНО! Временное ограничение движения автотранспортных средств в Димитровграде
- Тарифы на электроэнергию для майнеров предложено повысить
Содержание |
[править] Maxima: укротитель выражений
Часть 3 Сегодня Тихон Тарнавский расскажет вам о возможностях Maxima по укрощению упрощению выражений, содержащих рациональные, иррациональные и тригонометрические функции.
В этот раз я расскажу о штатных возможностях Maxima по упрощению и прочим преобразованиям выражений. В частности, речь пойдет об автоматическом раскрытии скобок и вынесении за скобки; об упрощении как арифметических действий над некоторыми элементами, так и выражений с участием степенных, показательных и логарифмических функций; а также об обработке тригонометрических выражений. Все эти функции призваны облегчать читаемость математических формул и повышать простоту их восприятия, а посему стоит уделить этому уроку достаточно внимания: при верном использовании данные манипуляции позволят сэкономить в процессе работы значительное количество времени.
[править] Выражаясь рационально...
Существенная часть интересующих нас сегодня функций предназначена для преобразования рациональных выражений. Напомню, рациональным называется выражение, состоящее только из арифметических операторов и возведения в натуральную степень; естественно, элементы такого выражения могут содержать и неарифметические и нестепенные функции – тогда такие элементы с точки зрения рационального выражения считаются атомарными, т.е. неделимыми и непреобразуемыми.
Функции, работающие с рациональными выражениями, описаны в разделе документации «Polynomials»; потому как рациональные функции с математической точки зрения рассматриваются как расширение многочленов (полиномов) – примерно так же, как рациональные числа считаются расширением целых (многочлены, кстати, тоже иногда называют целыми функциями; хотя общий математический смысл этого термина несколько шире).
Имена всех функций Maxima по обработке рациональных выражений содержат буквосочетание rat, но не от слова «крыса», а от слова «rational». И начнем мы знакомство с ними с функции, которая так и называется: rat(выражение). Эта функция преобразовывает рациональное выражение к так называемой канонической форме (Canonical Rational Expression, CRE). То есть раскрывает все скобки, затем приводит все к общему знаменателю, суммирует и сокращает; кроме того, приводит все числа в конечной десятичной записи к рациональным.
Тут надо заметить, что атомарные элементы, т.е. символы и числа, в канонической форме рационального выражения в Maxima имеют другое внутреннее представление. При работе в интерфейсах Maxima и xMaxima об этом напоминает приписка /R/ после имени ячейки вывода (в wxMaxima и TeXmacs такая приписка отсутствует). При этом внешне, на видимом пользователю уровне, каноническая форма ничем, кроме этого обозначения, от общей не отличается. Но один достаточно интересный момент здесь есть: если каноническая форма рационального выражения используется в других рациональных выражениях, то последние также автоматически приводятся к канонической форме:
Это может быть достаточно удобно, если вам нужно пошагово проделать большое количество рациональных преобразований: вы можете, один раз вызвав rat(), ссылаться на предыдущие ячейки и благодаря этому далее автоматически видеть на каждом шаге итоговое выражение в канонической, а значит, достаточно компактной и удобной к восприятию, форме. Если на каком-то этапе такое поведение станет вам мешать, вы можете вернуть выражение из канонической к общей форме с помощью функции ratdisrep(выражение). Кроме того, каноническая форма автоматически «отменяется» и в случае любых преобразований, не являющихся рациональными:
Здесь, хотя %o2 было выражением в канонической форме, %o3 – уже выражение общего вида, так как оно не является рациональным.
Скажем пару слов о приведении конечной десятичной записи чисел к рациональной. Конечная десятичная запись считается по определению приблизительной, что и понятно, т.к. при вычислениях самой Maxima такая запись может возникнуть исключительно при применении приближенных методов либо при ручном указании о переводе числа в десятичную запись из математической, в результате чего результат тоже, вероятнее всего, окажется приблизительным. Эта приблизительность учитывается и при переводе в рациональные числа, а ее уровень, то есть мера, на которую рациональное число при переводе может отклониться от конечной десятичной записи, регулируется переменной ratepsilon, равной по умолчанию 2.0e-8, т.е. 0.00000002. Если такое положение вещей вас не устраивает, вы можете убедить Maxima оставлять десятичную запись чисел как есть, установив в true значение флага keepfloat (по умолчанию он равен false).
Следующая функция раскрывает скобки в рациональном выражении и называется ratexpand() (одно из значений слова expand и есть «раскрыть скобки»). Здесь также действует опция keepfloat. Кроме нее, есть еще одна опция – ratdenomdivide; по умолчанию она установлена в true, что приводит к тому, что каждая дробь, в которой числитель является суммой, распадается на сумму дробей с одинаковым знаменателем. Если же сбросить эту опцию в false, тогда все дроби с одинаковым знаменателем будут, напротив, объединены в одну дробь с числителем в виде суммы числителей изначальных дробей. То есть внешне результат будет в этом случае выглядеть почти так же, как и у функции rat(); к тому же единственная видимая пользователю разница проявляется только в рациональных выражениях от нескольких переменных (или различных иррациональных выражений). Заключается эта разница в том, что после ratexpand() и в числителе, и в знаменателе дроби все скобки будут раскрыты, в случае же rat() слагаемые, где присутствуют, скажем, две переменных, будут сгруппированы, и одна из них будет вынесена за скобки (в документации такая форма записи называется «рекурсивной» (recursive):
Кроме того, разница, конечно, заключается и во внутреннем представлении: с точки зрения программы, после ratexpand() выражение будет по-прежнему общего вида. Соответственно и все результаты дальнейших рациональных действий с выражением не будут автоматически «канонизироваться». Я специально обращаю ваше внимание на схожесть между результатами этих двух различных функций, поскольку в документации эта схожесть никак не обозначена: в описании обеих функций и примерах к ним нет вообще никаких ссылок друг на друга.
Помимо флага ratdenomdivide, есть также функция, собирающая воедино дроби с одинаковыми знаменателями; зовут ее combine():
В дополнение к функции ratexpand() есть также флаг ratexpand, который по умолчанию равен false, а будучи установлен в true, приводит к тому, что все рациональные выражения в канонической форме отображаются и преобразовываются к общему виду сразу же с раскрытыми скобками:
Обратите внимание, что при применении этого флага выражение сохраняет каноническую форму.
Действует в этом случае и флаг ratdenomdivide (напомню, что в строке %i1 этот флаг был установлен локально, используя сокращенную запись функции ev()):
Иными словами, флаг ratexpand по своему действию аналогичен одноименной функции, но действует он на все без исключения канонические рациональные выражения и при этом оставляет их в канонической внутренней записи и изменяет только внешнее отображение этой записи, сохраняя при этом и дальнейшую автоматическую «канонизацию».
[править] ...и не только рационально.
Помимо ratexpand() есть также и функция «просто» expand(). Различий между ними несколько, наиболее принципиальные таковы. Во-первых, ratexpand() раскрывает только рациональное выражение «верхнего уровня», все же подвыражения, не являющиеся рациональными, обрабатываются как атомарные, то есть внутрь них она не залезает; expand() же раскрывает скобки на всех уровнях вложенности:
Во-вторых, ratexpand() приводит дроби-слагаемые к общему знаменателю, а expand() этого не делает; в-третьих, на функцию expand не действует переключатель ratdenomdivide:
И в-четвертых, expand() не преобразовывает к рациональным числам конечную десятичную запись – опять-таки, вне зависимости от флага keepfloat.
Функция expand(), в отличие от своего рационального сородича, имеет несколько вариаций – в виде отдельных функций с похожими названиями, которые раскрывают скобки несколько по-разному. Первую мы уже рассмотрели. Вторая называется expandwrt(выражение, x, y, ..., v), где wrt расшифровывается как «with respect to...», то есть «относительно...». Она раскрывает скобки не везде, а только относительно тех символов, которые заданы в списке аргументов после выражения. Другими словами, только там, где из скобок можно вынести хотя бы один из перечисленных символов:
(На предупреждение, возникающее при первом вызове функций expandwrt*(), можете не обращать внимания – на функционале, о котором идет речь, оно никоим образом не отражается.)
Если в выражении встречаются дроби, то по умолчанию эта функция раскрывает скобки только в их числителях, оставляя знаменатели в покое. Изменить это поведение можно переключателем expandwrt_denom, установив его в true (по умолчанию он равен false):
И, наконец, последняя функция из этого семейства – expandwrt_factored(выражение, x, y, ..., v) – раскрывает скобки лишь в тех слагаемых, где упомянутые символы встречаются не в одном, а в каждом из сомножителей:
Раскрытием возведения в целую степень можно управлять как в контексте функции expand(), так и отдельно. В первом случае применяются переменные maxposex и maxnegex, определяющие соответственно максимальные положительный и отрицательный показатель степени, которые будут раскрываться этой функцией. По умолчанию оба параметра равны 1000. Переназначить их можно не только глобально, но и в контексте одного конкретного вызова функции expand() – в таком случае это делается с помощью дополнительных аргументов, задаваемых после выражения:
В противовес maxposex и maxnegex можно задать максимальные положительную и отрицательную степени, которые будут раскрываться автоматически, без вызова функций группы expand. За это отвечают переменные expop и expon, и по умолчанию они равны нулю, то есть автоматически степени не раскрываются вообще.
Кроме самостоятельной функции expand(), существуют также флаги expand и expand(p, n) у функции ev(). Запись выражение, expand равносильна expand(ev(выражение)), а выражение, expand(p, n) – expand(ev(выражение, p, n)).
Возможности управлять раскрытием скобок на этом не заканчиваются. Еще одна функция – distrib() – представляет как бы облегченный вариант expand(). Она действует аналогично expand(), но только на один уровень в глубину:
В противоположность функциям *expand*(), раскрывающим скобки, можно также и разложить выражение на множители, то есть максимально повыносить все за скобки. Делается это с помощью функции factor():
Если функции factor() передать целое число, она разложит его на простые множители; если же передать рациональное число – на множители будут разложены его числитель и знаменатель:
Если многочлен не может быть представлен в виде произведения нескольких сомножителей, его можно попытаться преобразовать в сумму таких произведений с помощью функции factorsum():
Функция factorsum() умеет раскладывать на множители только независимые слагаемые, то есть такие, которые не содержат одинаковых переменных. Если мы раскроем скобки в выражении, содержащем в двух разных местах один и тот же символ, то так как коэффициенты при этом символе после раскрытия сгруппируются, factorsum() не сможет понять, каким именно образом разгруппировать их обратно:
Нужно заметить, что функции factor() и factorsum(), хотя и не имеют в имени приставки rat, все же ведут себя в смысле разбора передаваемых им выражений не как expand() и сопутствующие, а как ratexpend(); то есть на любой не-рациональной функции останавливаются и внутрь не идут:
Впрочем, об этом можно догадаться из документации, так как функции factor* описаны не в разделе Simplification, куда относятся expand*, а, так же, как и rat*, в разделе Polynomials.
Выносить за скобки, а также раскрывать эти скобки можно не только специальной функцией, но и дополнительным флагом ко все той же канонической форме рациональных выражений. Флаг этот зовут ratfac, и по умолчанию он равен false, то есть вынесение за скобки не происходит. Если же его установить в true, то в каждом рациональном выражении, приведенном к канонической форме, все будет максимально вынесено за скобки, но без вызова функции factor(); например, в примере ниже не произошло обратного свертывания (x+1)2, хотя, будучи применен к первоначальному выражению, флаг ratfac сохранил и этот множитель нераскрытым (также можете сравнить этот пример с аналогичным примером к функциям ratexpand() и rat()):
[править] Проще простого
Итак, о преобразованиях выражений мы уже поговорили достаточно – теперь перейдем к их упрощению. Об элементарных упрощениях мы уже говорили в предыдущий раз: они могут производиться автоматически, на что влияет установленный флаг simp; и по умолчанию именно так и происходит.
Здесь тоже все начинается с рациональных выражений, которыми занимается функция ratsimp(выражение). Она упрощает выражение за счет рациональных преобразований, но, в отличие от остальных функций по обработке рациональных выражений, работает в том числе и «вглубь», то есть иррациональные части выражения не рассматриваются как атомарные, а упрощаются, в том числе, и все рациональные элементы внутри них:
На ratsimp() действуют те же флаги, что и на rat(): и ratexpand, и keepfloat, и ratfac. Но отличается она от rat() или ratexpand() не только умением работать «в глубину», но и некоторыми дополнительными рациональными преобразованиями, которые не поддерживаются этими двумя функциями:
Кроме функции ratsimp(), есть еще и дополнительный переключатель – ratsimpexpons. По умолчанию он установлен в false; если же назначить ему значение true – это приведет к автоматическому упрощению показателей степени:
Функция ratsimp() – это уже достаточно мощный, и в то же время весьма быстрый, механизм упрощения; но, конечно, не достаточный: ведь те действия, которые можно упростить в разнообразных математических выражениях, не ограничиваются рациональными. Поэтому все же основной плюс этой функции – это скорость. А для более серьезных упрощений существует расширенный вариант – fullratsimp(выражение). Эта функция последовательно применяет к переданному выражению функцию ratsimp(), а также некоторые нерациональные преобразования – и повторяет эти действия в цикле до тех пор, пока выражение не перестанет в процессе них изменяться. За счет этого функция работает несколько медленнее, чем ratsimp(), зато дает более надежный результат – к некоторым выражениям, которые она может упростить с ходу, ratsimp() пришлось бы применять несколько раз, а иногда та и вообще не справилась бы с задачей.
И третья основная функция упрощения выражений – уже никак с предыдущими двумя не соотносящаяся – radcan(выражение). Если ratsimp() и fullratsimp() ориентированы на упрощение рациональных действий, то radcan() занимается упрощением логарифмических, экспоненциальных функций и степенных с нецелыми рациональными показателями, то есть корней (радикалов). Например, выражение из второго примера в этом разделе radcan() сможет упростить сильнее, чем ratsimp()/fullratsimp():
В некоторых случаях наилучшего результата можно добиться, комбинируя radcan() с ratsimp() или fullratsimp().
С функцией radcan() смежны по действию еще два управляющих ключа. Один из них называется %e_to_numlog. Влияет он не на саму функцию, а на автоматическое упрощение. Если выставить его в true, то выражения вида e(r*log(выражение)), где r – рациональное число, будут автоматически раскрываться в выражениеr. Функция radcan() делает такие преобразования независимо от значения ключа. Второй ключ – radexpand (от radical, не путать с ratexpand) – влияет на упрощение квадратного корня из четной степени какого-либо выражения. Он, в отличие от большинства переключателей, имеет не два, а три значения: при значении all, sqrt(x2) будет раскрываться в x – как для действительных, так и для комплексных чисел; при значении true (по умолчанию), sqrt(x2) для действительных чисел превращается в |x|, а для комплексных не преобразуется; а при значении false, sqrt(x2) не будет упрощаться вообще.
Следующие две функции и один флаг относятся к упрощению факториалов. Функция factcomb(выражение) проводит упрощения вида n!*(n+1) = (n+1)! и тому подобные. Функция minfactorial, напротив, сокращает факториалы, то есть действует по принципу n!/(n–1)! = n. И флаг sumsplitfact, который изначально установлен в true, находясь в состоянии false, приводит к тому, что после того, как отработает factcomb, minfactorial вызывается автоматически.
[править] Вот под таким углом...
И напоследок поговорим о функциях для преобразования тригонометрических формул. Здесь так же, как и у рациональных функций, присутствует общая для всех приставка – trig; расшифровывать ее, думаю, особой нужды нет. Начнем по традиции с функции trigexpand(выражение). Она, как нетрудно догадаться, раскрывает скобки в тригонометрических выражениях:
Здесь, как обычно, есть несколько управляющих флагов, первый из которых опять же является тезкой самой функции. Он приводит к повторному раскрытию всех синусов-косинусов, то есть фактически равнозначен повторному вызову самой функции:
Второй флаг – halfangles – управляет раскрытием формул половинных углов. Оба эти флага по умолчанию сброшены. А следующие два флага – trigexpandplus и trigexpandtimes – отвечают соответственно за применение формул сумм углов и кратных углов. То есть в примере выше сначала сработал флаг trigexpandplus, а затем – trigexpandtimes. Эти флаги по умолчанию установлены, что и видно из примера.
Кроме всего уже упомянутого, есть еще флаги trigsign и triginverses. Первый принимает традиционные два значения (по умолчанию – true) и регулирует вынос знака за пределы тригонометрической функции, то есть, к примеру, sin(–x) упростится до –sin(x), а cos(–x) – до cos(x). Флаг triginverses – трехзначный, и умолчательное его значение равно all. Он отвечает за обработку сочетаний вида sin(asin(x)) или atan(tan(x)). Значение all позволяет раскрывать эти сочетания в обоих направлениях (напомню, что при этом часть корней будет теряться); значение true оставляет разрешенным раскрытие только вида sin(asin(x)), то есть блокирует вариант с потерями периодических значений; а случай false запрещает оба направления преобразований.
Функция, обратная trigexpand(), называется trigreduce(выражение) – здесь, в полном соответствии со значением слова reduce, действуют формулы понижения степени. Например, применив дважды эту функцию к результату предыдущего примера, мы получим его в исходном виде (см. рис. наверху страницы).
Эту функцию можно вызвать с более полным списком аргументов: trigreduce(выражение, переменная) – тогда формулы понижения степени будут применяться только по отношению к заданной переменной (переменная может быть, как и почти везде, не только отдельным символом, но и выражением).
Третья функция занимается уже упрощением, и зовут ее, соответственно, trigsimp(выражение). Она старается упростить любое тригонометрическое выражение, используя известные формулы, такие как sin2(x)+cos2(x)=1 и тому подобные. Для наилучшего результата ее можно комбинировать с trigreduce(), ratsimp()/fullratsimp() и radcan().
Этим возможности Maxima по преобразованию и упрощению разнообразных выражений еще не совсем исчерпаны, но основные из них мы рассмотрели в полной мере. В следующий раз поговорим немного о применении некоторых встроенных функций, о работе с векторами, матрицами и множествами и, возможно, о работе с логикой, с уравнениями и неравенствами, а также их системами.